이번에는 시스템의 선형 근사화에 많이 사용하는 데일러 급수 전개를 이야기하려고 합니다. 수학적 증명을 다룰려는 것은 아니구요. 그냥 테일러 급수 전개식을 소개하고 어떻게 사용하는지를 이야기하고, 테일러 급수 전개를 한 결과가 원 함수와 얼마나 비슷한지를 파이썬으로 확인해보려고 합니다.
이전 강의
이 글은 스프링 매스 댐퍼 시스템을 소개하던 글에 이어서
[Control System 기초] Spring Mass Damper 시스템 소개
이번에는 제어시스템에서 기초 중에 기초가 되는 Spring Mass Damper 시스템을 소개하려고 합니다. 제어공학에서 가장 기초가 되는 모델이지요. 지금 위의 그림이 스프링-매스-댐퍼 시스템을 간략히
pinkwink.kr
선형시스템에 대해 이야기한 글
[Control System 기초] Linear System이라는 말의 뜻
오늘은 Spring Mass Damper시스템을 예시로 간단한 미방으로 시스템이 꾸며진다는 것을 이야기했는데요. 이번에는 선형시스템, 제어공학에서 이야기하는 선형시스템 Linear System이 어떤 것인지를 또
pinkwink.kr
에 이어지는 글입니다.
테일러 급수 전개

어떤 함수 g(x)가 있다면 이 함수를 동작점(x0) 근처에서 테일러 급수 전개를 하면

이렇게 표현할 수 있습니다. 동작점을 입력으로 함수에 넣은 값에서 출발해서 미분을 여러차례한 계수와 급수전개를 한 항을 계속 이어서 표현하는 형태입니다. 우리가 흔히 선형 근사화를 한다고 하면 한 번 미분한 것만 사용하게 됩니다.

이 첫 항만 사용하면 1차식으로 근사화할 수 있게 되거든요.
진자 시스템의 토크식에 적용

이렇게 생긴 시스템이 있다고 보겠습니다. 진자(pendulum)가 실에 매달려 흔들거리는 거죠. 이때 질량(M)이 있는 진자는 접선의 방향으로 힘을 가지게 됩니다. 접선에 수직한 방향으로의 힘은 실의 장력과 함께 사라지구요.
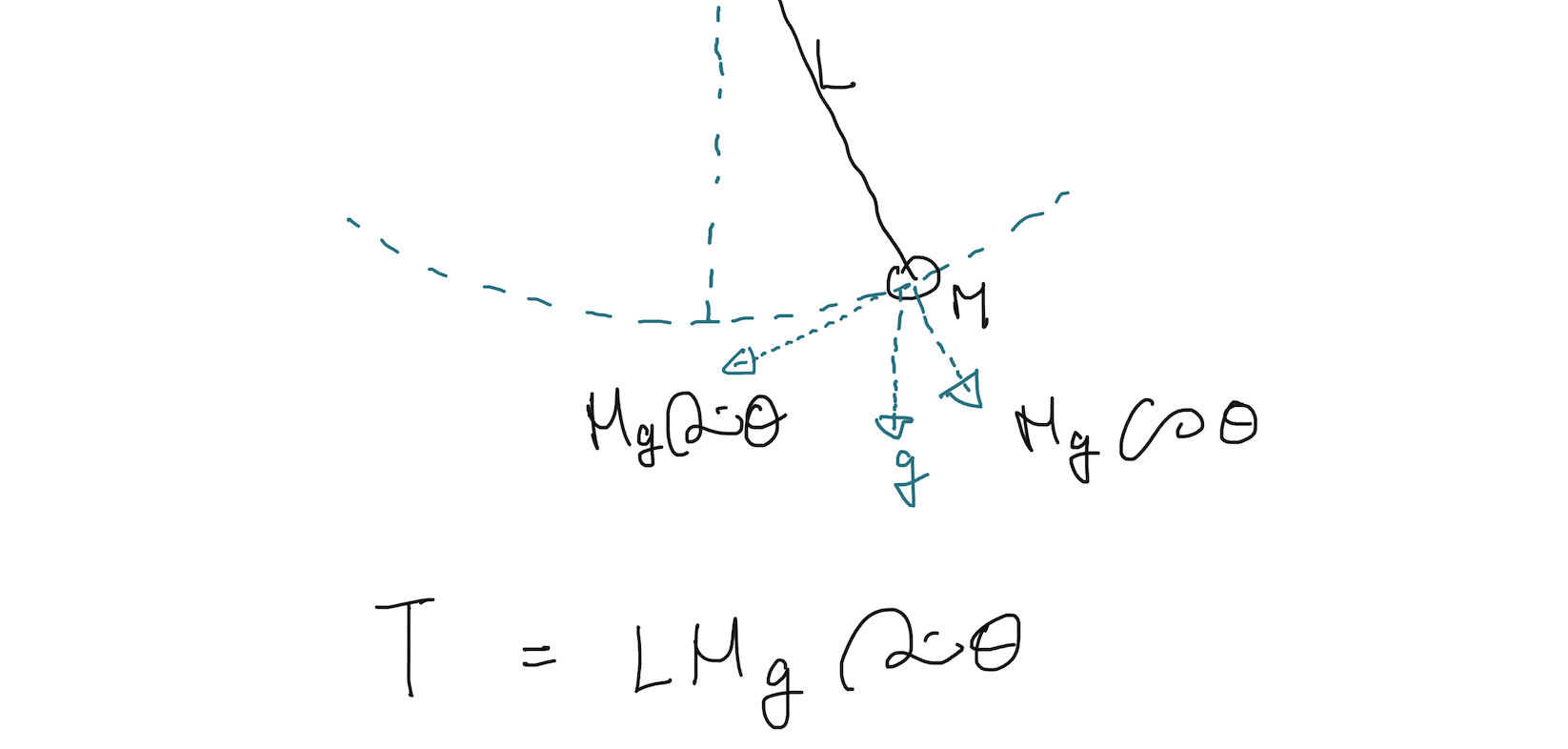
그러면 토크(T)는 위 식처럼 표현할 수 있고, LMg를 그냥 1이라고 가정해버리면, 진자의 토크 식은

이렇게 심플하게 sin으로 표현할 수 있습니다. 지금은 테일러 급수전개를 다룰거라 여~~~러가지를 그냥 생략했습니다. 이제 sin 함수를 테일러 급수전개를 3번째 미분하는 항까지 진행해보면

이 됩니다. 동작점을 0으로 볼거라사 sin 0은 다 0이 되니 남은 항은

이렇게 됩니다. 위 식은 3번째 테일러항까지 본것이구요. 저렇게까지 안하지만 조금있다가 코드에서 다룰거라 한 번 적었습니다. 선형 근사화만 하면~

가 됩니다.
Python으로 이해해보기
먼저
import numpy as np
import matplotlib.pyplot as plt
theta = np.arange(-2, 2, 0.01)
T = np.sin(theta)
plt.figure(figsize=(10,10))
plt.plot(theta, T)
plt.grid()theta를 -2부터 2까지로 보고 sin(theta)를 준비합니다.

이렇게 생겼죠. 여기에 1차 근사화까지 한 테일러 급수 전개 결과는 T=theta였습니다. 그것을 같이 그려 보겠습니다.
tayler_1 = theta
plt.figure(figsize=(10,10))
plt.plot(theta, T, label='sin')
plt.plot(theta, tayler_1, label='tayler 1')
plt.legend()
plt.xlim(-1,1)
plt.ylim(-1,1)
plt.grid()
0부근에서는 정말 비슷한 값을 가지는것을 알 수 있습니다. 동작점 부근에서 선형 근사화를 해도 괜찮을 것 같다는 생각이 드시나요. 이번에는 3번째 미분항까지 진행한것도 함께 그려보도록 하겠습니다.
tayler_3 = theta - 1/6*theta**3
plt.figure(figsize=(10,10))
plt.plot(theta, T, label='sin')
plt.plot(theta, tayler_1, label='tayler 1')
plt.plot(theta, tayler_3, label='tayler 3')
plt.legend()
plt.xlim(-1,1)
plt.ylim(-1,1)
plt.grid()
파란선과 녹색선이 거의 겹쳐 있죠. 이렇게 보면 확실히 동작점 부근에서 원함수를 테일러 급수 전개는 잘 표현한다고 볼 수 있습니다. 보통은 선형근사화에 사용하지만 말이죠.
동영상 강의
'Theory > ControlTheory' 카테고리의 다른 글
| [Control System 기초] Linear System이라는 말의 뜻 (2) | 2022.04.04 |
|---|---|
| [Control System 기초] Spring Mass Damper 시스템 소개 (5) | 2022.03.25 |
| Python으로 수행하는 주파수 분석 - FFT, STFT (6) | 2022.02.09 |
| Python class로 만드는 1차 저역통과필터 Low Pass Filter (10) | 2021.03.19 |
| [필터연재] 2차 디지털 Band Pass, Band Stop 필터 (18) | 2017.01.11 |
| [필터연재] 2차 디지털 저역/고역 통과필터 (18) | 2017.01.06 |
| [필터연재] 1차 디지털 저역/고역 통과필터 (17) | 2017.01.05 |



