디지털 필터에 대해서는 예전에 많이 다루었는데요. 당시에 다룰때는 간단히 Python의 함수(def)를 사용해서 많이 다루었습니다. 이번에는 class를 이용해서 조금 사용성을 높인 코드를 보여드리는 것이 어떨까하고 글을 작성합니다. 일단 1차 저역통과필터는 예전에 소개한 글에서 수식을 가져오겠습니다.

저 식을 코드로 단순 변환 시켜보면
out = (tau * pre_out + ts * data) / (tau + ts)입니다. 수식에서 분모가 같으니 tau + ts는 빼서 보면 저렇게 되죠. 문제는 pre_out입니다. 현재 출력값 out, 수식에서는 yn의 이전 값이거든요. 그래서 저 코드가 실행된 직후 현재 출력을 별도로 저장해야 합니다. 만약 class를 사용하지 않는다면, 1차 저역통과필터가 필요할때마다 만들어야할 변수 때문에 고생을 하겠죠. 저 핵심 코드를 코함해서 간단히 클래스로 만들어 보겠습니다.
import numpy as np
class LowPassFilter:
def __init__(self, cutoff_freq, ts):
self.ts = ts
self.cutoff_freq = cutoff_freq
self.pre_out = 0.
self.tau = self.calc_filter_coef()
def calc_filter_coef(self):
w_cut = 2*np.pi*self.cutoff_freq
return 1/w_cut
def filter(self, data):
out = (self.tau * self.pre_out + self.ts * data) / (self.tau + self.ts)
self.pre_out = out
return out어떤가요. 입력 부분만 조금 편하게 Hz 단위의 차단 주파수를 넣었습니다. 선언하는 방법은
lpf = LowPassFilter(cutoff_freq = 0.5, ts = 0.01)이렇게 차단 주파수를 0.5Hz로 샘플링타임을 0.01로 잡아주면 되겠죠. 필터를 한 번 테스트해보겠습니다.
import matplotlib.pyplot as plt
%matplotlib inline
t = np.arange(0, 10, 0.01)
y = np.sin(t)
plt.plot(t, y);간단하게 0부터 10초까지 0.01초 간격으로 sin 함수를 만들어 둡니다.

이렇게 생겼습니다. 이제 잡음을 살짝 입히도록 하죠
y = 10*np.sin(t) + 5*np.random.rand(len(y))
plt.plot(t, y);이렇게 두겠습니다. 이 결과는
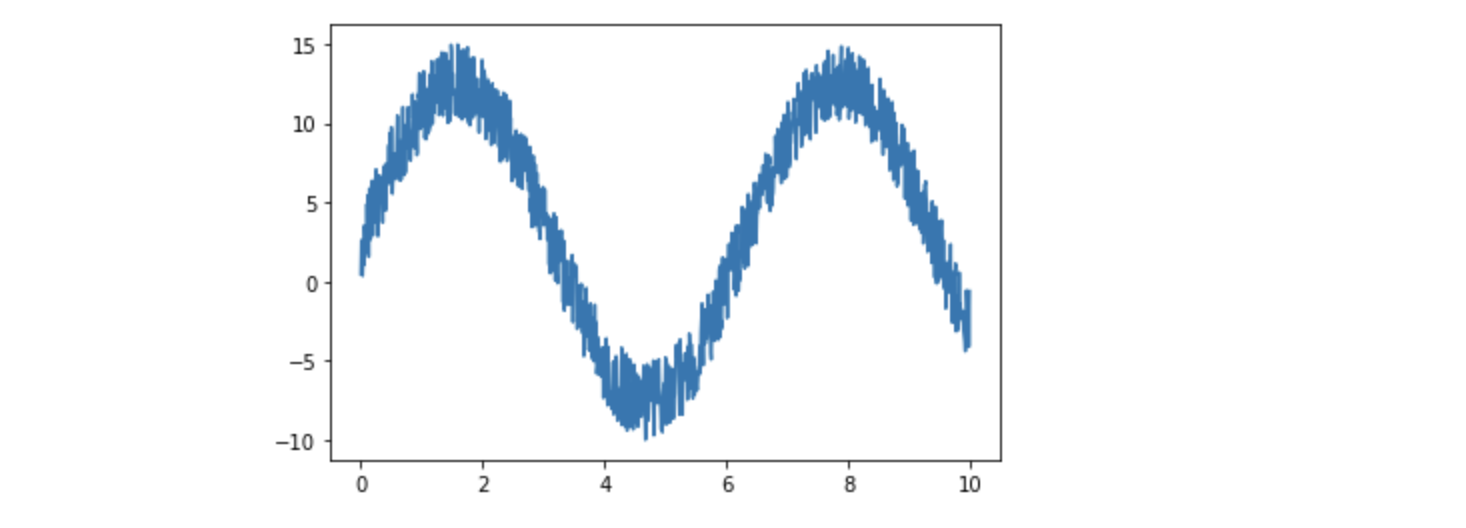
이렇게 생겼습니다. 이제 아까 선언해둔 lpf를 적용시켜보죠.
filtered_data = [lpf.filter(data) for data in y]
plt.plot(t, y)
plt.plot(t, filtered_data, 'r', lw=3);코드는 이렇게 사용하면 됩니다. 이제 결과를 보겠습니다.

타임 딜레이가 있지만, 연습용이니까요.^^. 0.5Hz 차단 주파수는 역시 좀 심했군요^.^ 아무튼 노이즈 들어간 신호를 잘 잡았네요. 이제 저역통과필터가 필요하신 분들은 위 class를 가져다 사용하시면 되겠습니다.^^
'Theory > ControlTheory' 카테고리의 다른 글
| [Control System 기초] Linear System이라는 말의 뜻 (2) | 2022.04.04 |
|---|---|
| [Control System 기초] Spring Mass Damper 시스템 소개 (5) | 2022.03.25 |
| Python으로 수행하는 주파수 분석 - FFT, STFT (6) | 2022.02.09 |
| [필터연재] 2차 디지털 Band Pass, Band Stop 필터 (18) | 2017.01.11 |
| [필터연재] 2차 디지털 저역/고역 통과필터 (18) | 2017.01.06 |
| [필터연재] 1차 디지털 저역/고역 통과필터 (17) | 2017.01.05 |
| 2차계 시스템의 응답 특성 간편히 확인해 보기 (11) | 2016.08.29 |