아주 예전에 Python으로 수행하는 FFT라는 주제의 글을 작성한 적이 있습니다. 이번에는 이 글에서 조금 더 나가서 STFT라는 개념도 이야기를 해 보려고 합니다. 시간영역에서의 신호를 분석할 때 많이 사용하는 것이 FFT인데요. 여기서 시간 구간에 대한 한계를 만날 수 있기 때문에 STFT Short Time Fourier Transform을 사용합니다. 오늘은 이 이야기를 해 보려고 합니다.
Python에서 수행해 본 간단한 FFT 코드
일요일 아침(이 글은 평일에 예약 발행되겠지만)이네요.. 오늘 아침은 꽤 상쾌하고 약간 몽롱한.. 뭐 아무튼 기분이 좋아지는 아침이네요^^. 요즘은 뭔가를 마무리하는 단계에서 오는 급급하게
pinkwink.kr
시험 데이터 만들기
일단 학습을 위해 필요한 데이터를 만들어 두도록 하겠습니다.
import numpy as np
import matplotlib.pyplot as plt
def sin_wave(amp, freq, time):
return amp * np.sin(2*np.pi*freq*time)먼저 numpy를 이용해서 삼각함수를 다소 간단한 형태로 정의 해 두겠습니다.

위 식을 코드로 구현한 것으로 f는 Hz 단위의 주파수입니다.
time = np.arange(0, 10, 0.001)
sin1 = sin_wave(1, 10, time)
sin2 = sin_wave(2, 5, time)
sin3 = sin_wave(4, 1, time)이제 시간 간격을 0.001(=1 milli-sec)로 두고 0초 부터 10초까지 시간(time)을 변수로 정의했습니다. 그리고 크기가 각각 1, 2, 4이고 주파수가 각각 10, 5, 1Hz가 되도록 sin1, sin2, sin3라는 데이터를 만들어 두었습니다. 각 데이터는 time에 의해 시간축 길이는 10초입니다.
plt.figure(figsize=(12,5))
plt.plot(time, sin1, label=r"$\sin {20\pi} t$", color='red')
plt.plot(time, sin2, label=r"$2\sin {10\pi} t$", color='blue')
plt.plot(time, sin3, label=r"$4\sin {2\pi} t$", color='green')
plt.legend(); plt.grid(); plt.show()이 시험용 데이터가 어떻게 생겼는지 확인해보도록 하죠. 간단히 matlplotlib로 그리고 label을 LaTeX로 달아 두었습니다.

저렇게 생긴 아이입니다. 크기와 주파수를 보면 쉽게 세 개의 신호가 확인이 될겁니다.
sin_sum = sin1 + sin2 + sin3
plt.figure(figsize=(12,5))
plt.plot(time, sin_sum)
plt.grid()
plt.show()이제 앞 서 만든 세 개의 신호를 더해서 sin_sum이라는 변수에 두었습니다. 그런데 이렇게 세 개의 신호를 더 하면 어떤 일이 생길까요?
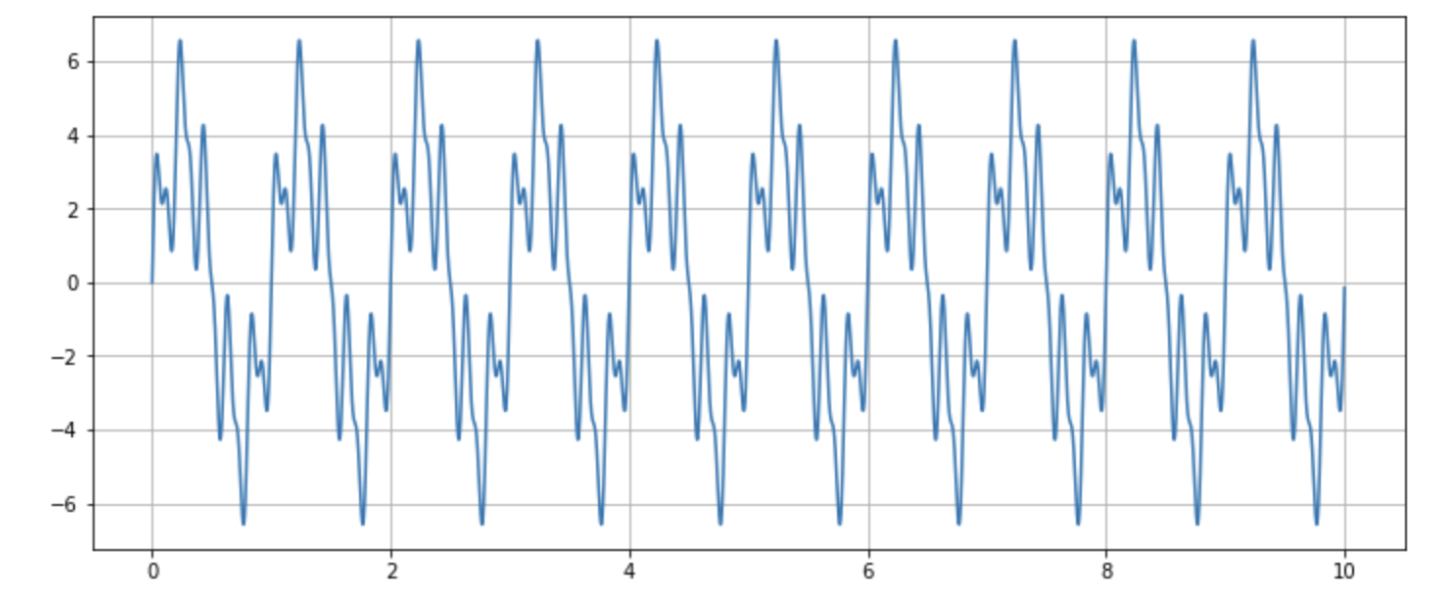
넵 이렇습니다. 뭔가 신기하지 않나요? 만약 이 신호의 출력이 신기해 보인다면 여러분들은 공대 체질일 지도 모릅니다^^
plt.figure(figsize=(12,7))
plt.plot(time, sin1, label=r"$\sin {20\pi} t$", color='green', alpha=0.5)
plt.plot(time, sin2, label=r"$2\sin {10\pi} t$", color='blue', alpha=0.5)
plt.plot(time, sin3, label=r"$4\sin {2\pi} t$", color='magenta', alpha=0.5)
plt.plot(time, sin_sum, label="sum_of_sin", color='black', lw=0.8)
plt.legend(); plt.grid(); plt.show()네 개의 신호를 모두 한 번에 그려보죠.
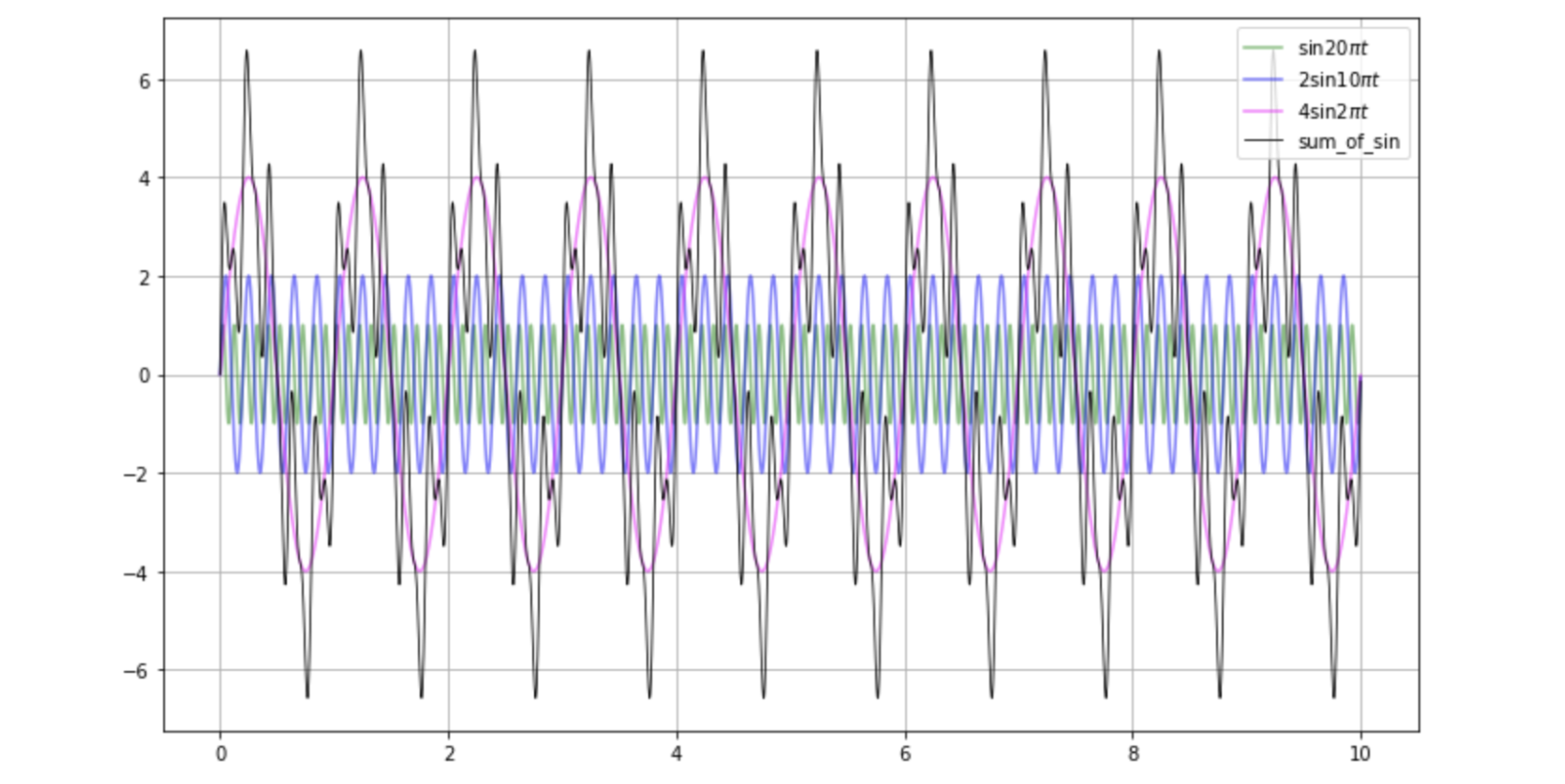
가장 느린 주파수(1Hz)인 신호 위에 높은 주파수의 성분이 실려서 sin_sum이라는 신호가 만들어진 것처럼 보이나요.
FFT를 이용한 주파수 분석

위 그림은 위키백과의 FFT 문서에 있는 그림입니다. 어떤 파형이 다양한 주파수 성분의 정현파로 표현할 수 있음을 보여주는 좋은 그림입니다. 빨간색으로 된 복잡해 보이는 신호는 삼각함수로 이뤄진 여러 파형으로 설명할 수 있음을 알 수 있습니다.
n = len(sin_sum)
k = np.arange(n)
Fs = 1/0.001
T = n/Fs
freq = k/T
freq = freq[range(int(n/2))]일단 sin_sum 데이터의 길이 만큼에 샘플 타임(1ms)의 역수를 취하면 구할 수 있는 샘플 주파수 1kHz를 구하고(Fs), 길이(n)로 나누면 주파수 영역의 간격을 계산할 수 있습니다. 그렇게 구한 freq라는 주파수 영역을 사용합니다.
Y = np.fft.fft(sin_sum)/n
Y = Y[range(int(n/2))]그리고 numpy가 제공하는 fft기능을 이용해서 sin_sum이라는 시간영역에서의 데이터에서 주파수 성분을 찾게 됩니다. 애초에 sun_sum은 1, 5, 10Hz의 신호들을 합친것이니 그런 결과가 나와야겠죠.
fig, ax = plt.subplots(2, 1, figsize=(12,8))
ax[0].plot(time, sin_sum)
ax[0].set_xlabel('Time')
ax[0].set_ylabel('Amplitude'); ax[0].grid(True)
ax[1].plot(freq, abs(Y), 'r', linestyle=' ', marker='^')
ax[1].set_xlabel('Freq (Hz)')
ax[1].set_ylabel('|Y(freq)|')
ax[1].vlines(freq, [0], abs(Y))
ax[1].set_xlim([0, 20]); ax[1].grid(True)
plt.show()sin_sum과 그 주파수 분석 결과인 Y(인데 복소수라 절대값으로)를 동시에 그려보면,

이렇습니다. 어떤가요? 위 그래프는 sin_sum이구요. 그 밑에 그림... 어때요? 1, 5, 10Hz가 정확히 나타납니다. 특히, 그 크기 1, 2, 4의 절반이 정확히 보입니다. 이렇게 테스트 해보면 확실히 FFT라는 방식이 꽤 유용하다는 것도 알 수 있습니다.
신호 전체에 FFT를 적용하는 것의 한계
그럼 앞서서 수행한 FFT가 어떤 한계가 있는지를 한 번 확인해 보도록 하죠.
sin_concat = np.concatenate((sin1, sin2, sin3, sin_sum))일단 numpy의 concatenate 명령은 신호를 이어서 붙이는 방식으로 합치는 겁니다. sin1, 2, 3과 sin_sum을 단지 시간 순서대로 합쳤기 때문에,
time = np.arange(0, 40, 0.001)
plt.figure(figsize=(12,5))
plt.plot(time, sin_concat)
plt.grid()
plt.show()그려보면~

이렇게 생겼습니다. 시간대별로 주파수의 성분이 확실히 다른 거죠.
n = len(sin_concat)
k = np.arange(n)
Fs = 1/0.001; T = n/Fs
freq = k/T
freq = freq[range(int(n/2))]
Y = np.fft.fft(sin_concat)/n
Y = Y[range(int(n/2))]
fig, ax = plt.subplots(2, 1, figsize=(12,8))
ax[0].plot(time, sin_concat)
ax[0].set_xlabel('Time')
ax[0].set_ylabel('Amplitude'); ax[0].grid(True)
ax[1].plot(freq, abs(Y), 'r', linestyle=' ', marker='^')
ax[1].set_xlabel('Freq (Hz)')
ax[1].set_ylabel('|Y(freq)|')
ax[1].set_xlim([0, 20])
ax[1].vlines(freq, [0], abs(Y)); ax[1].grid(True)
plt.show()다시 FFT를 수행해 보았습니다.
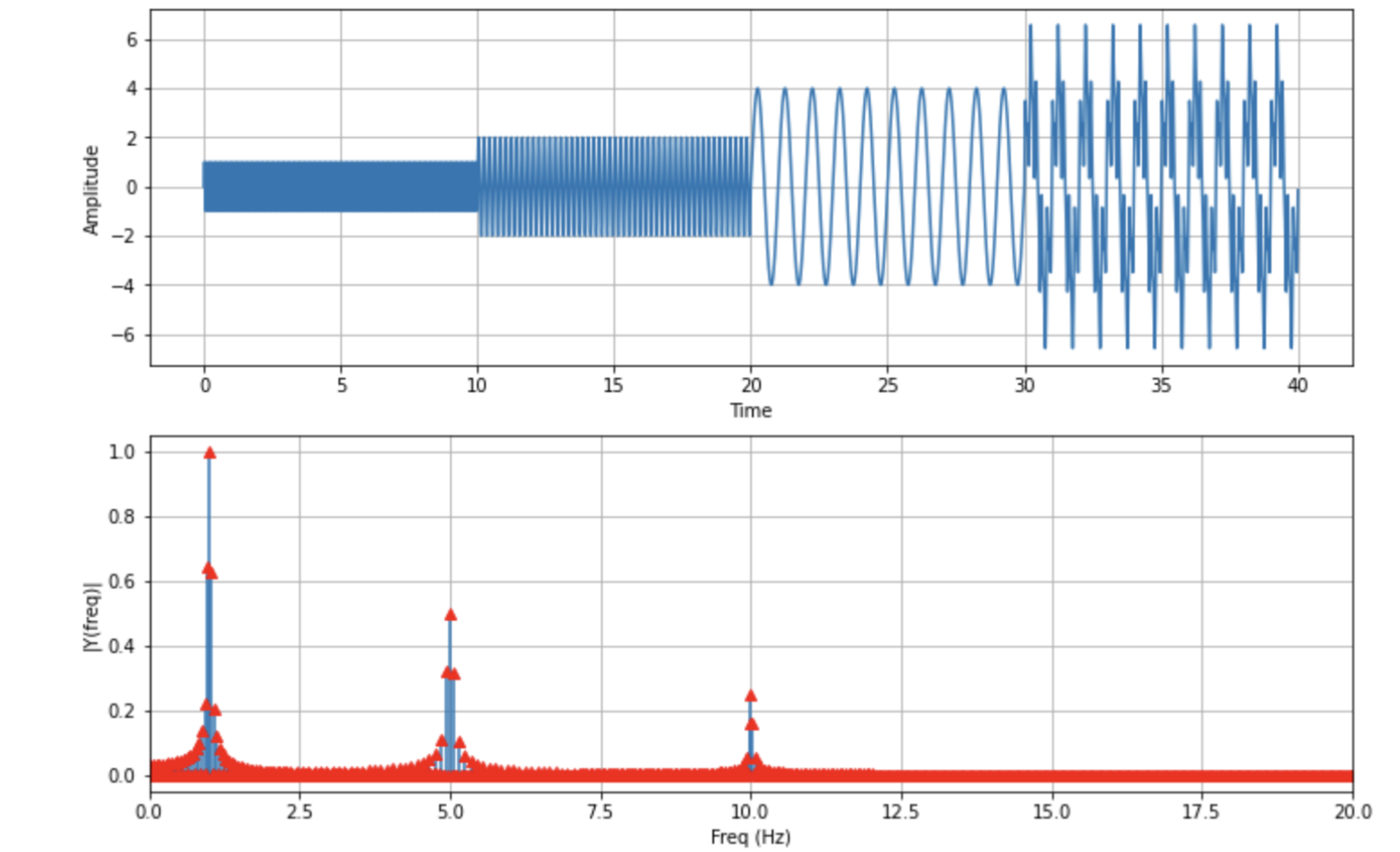
이렇게 1, 5, 10Hz의 주파수 성분이 나타났지만, 사실 시간대별로 완전히 다른 주파수 특성을 다 반영하지 못하고 있습니다. 그냥 신호 전체에서의 주파수 특성을 보여 주는 거죠. 이렇게 하고 싶지 않은 겁니다. 10초, 20초, 30초, 40초마다 다른 주파수 특성을 잘 보여주고 싶은 겁니다.
Short Time Fourier Transform - STFT
앞서서의 이유로 시간 영역 전체 기간동안 FFT를 하는 것은 원하는 결과를 얻지 못 할 수 있습니다. 그래서 나타난 것이 시간 영역을 짧게 끊어서 각 영역마다 FFT를 수행하는 개념이 나타납니다.
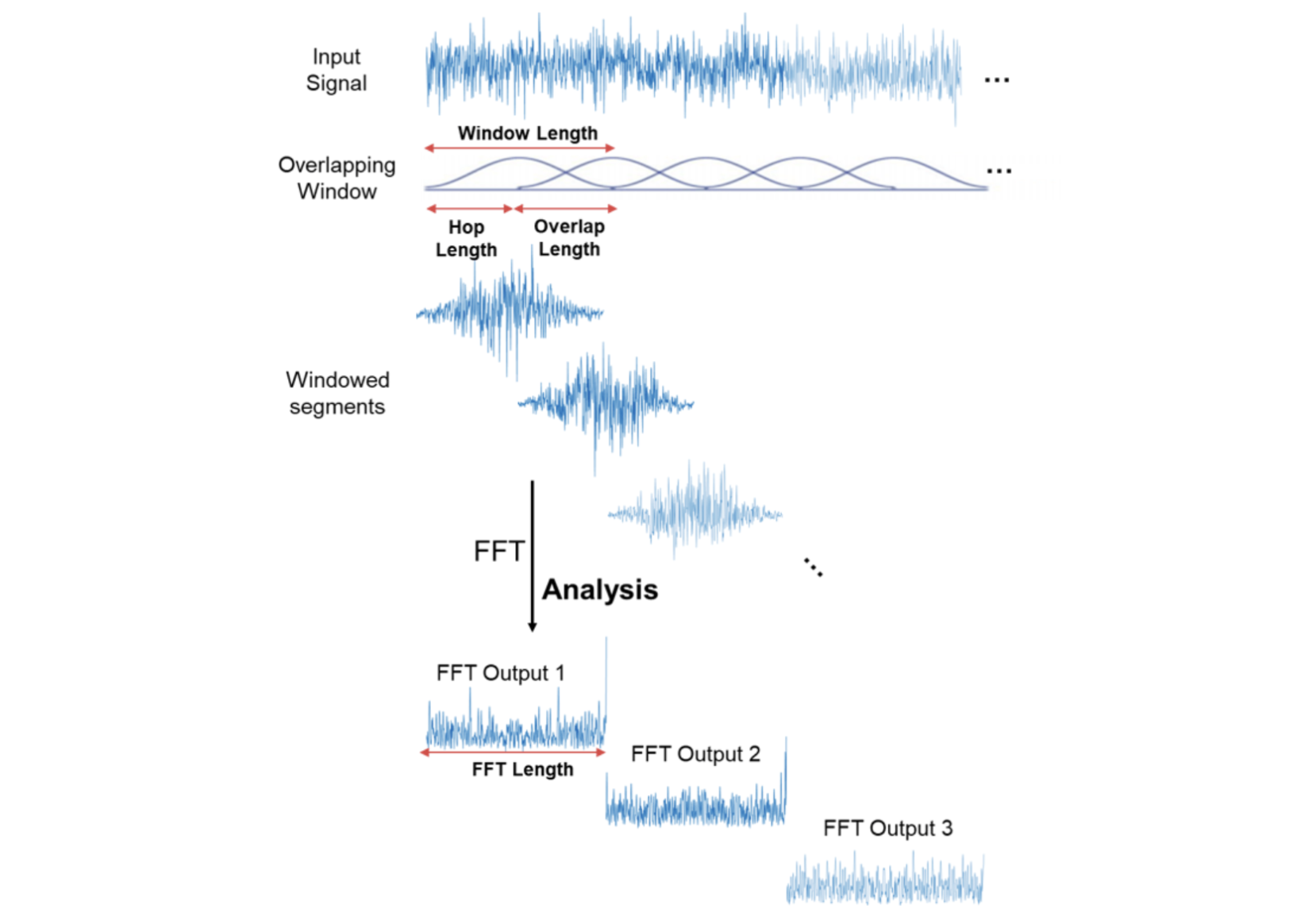
위 그림을 보면 Window Length와 Overlap Length를 정해서 짧은 구간 끊어서 각각 FFT를 수행하는 것입니다.
def draw_stft(f, t, Zxx):
plt.figure(figsize=(12,5))
plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=1, shading='gouraud')
plt.title('STFT Magnitude'); plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]'); plt.ylim([0, 20]); plt.show()앞서 이야기한 개념이 STFT인데 STFT를 수행한 결과를 pcolormesh라는 matplotlib의 함수를 이용해서 그릴겁니다.
from scipy import signal
def calc_stft(nperseg):
f, t, Zxx = signal.stft(sin_concat, Fs, nperseg=nperseg)
draw_stft(f, t, Zxx)STFT는 scipy에서 제공하는 함수를 사용하구요. nperseg라는 옵션이 window length를 결정하는 옵션이고, scipy의 stft 함수는 operlap 설정이 nperseg의 절반으로 잡는 것이 기본 설정입니다.
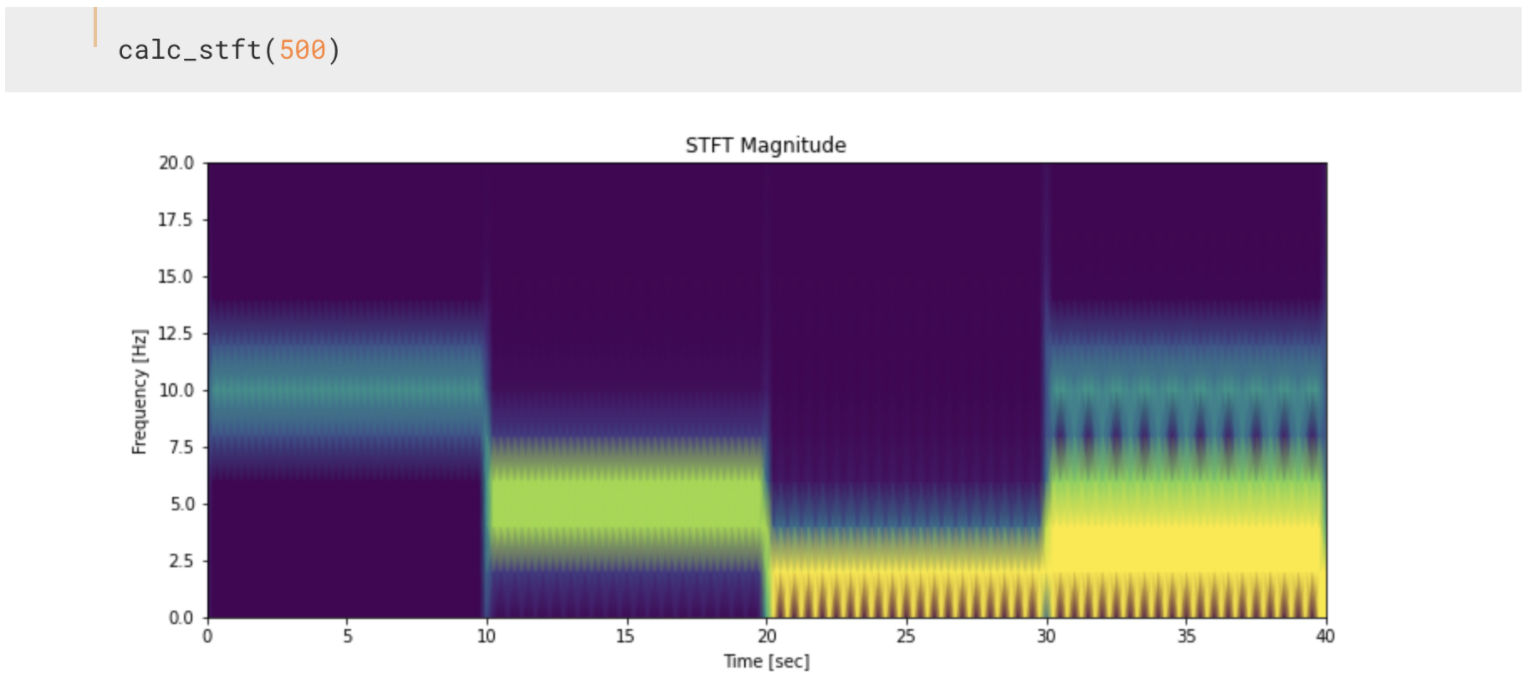
어떤가요 window length를 500개 샘플로 잡았더니 저렇게 시간대별 주파수 성분이 보입니다. 이렇게만 보면 어쩌면 잘 되었나하고 생각할 수도있지만 nperseg의 설정을 조금 바꿔보죠

이번에는 nperseg 설정을 높였습니다. 보다 주파수 성분이 선명해 지는 것을 볼 수 있습니다. 그럼 더 높을 수록 좋을까요?

그렇지는 않습니다. 10초, 20초 등등 경계선 지점을 보면 없던 주파수 성분이 있는 걸로 보이죠. 신호의 특성에 맞춰 스스로 window length는 잡아야 합니다.
마무리
이번 글에서는 예전에 다루었던 FFT를 이용해서 신호를 주파수 성분으로 변환하는 예제와 또 그 한계를 다루어 보았습니다. 그래서 그 한계를 극복하는 한 방법으로 STFT를 이야기를 했습니다. 이 글은 여기서 조금 더 이어서 다음 단계로 넘어가려고 하는데요. 일단 그건 다음에~^^ 아 혹시 푸리에 변환 자체게 완심이 있으신 분들은 아래의 글을 읽어보시기 바랍니다.
[선형변환] 푸리에 변환 Fourier Translation
본 자료는 국립 창원대학교 메카트로닉스 공학부 학생을 대상으로 한 선형변환 수업 자료입니다. 본 자료는 수업의 교재인 공업수학 (신윤기 저, 도서출판 인터비젼)의 내용을 재구성한 것으로
pinkwink.kr
그리고 이 내용은 혹시 필요하신 분이 있을까봐 영상으로도 공개됩니다.
'Theory > ControlTheory' 카테고리의 다른 글
| [Control System 기초] 테일러 급수 전개를 이용한 시스템 근사화 (2) | 2022.04.19 |
|---|---|
| [Control System 기초] Linear System이라는 말의 뜻 (2) | 2022.04.04 |
| [Control System 기초] Spring Mass Damper 시스템 소개 (5) | 2022.03.25 |
| Python class로 만드는 1차 저역통과필터 Low Pass Filter (10) | 2021.03.19 |
| [필터연재] 2차 디지털 Band Pass, Band Stop 필터 (18) | 2017.01.11 |
| [필터연재] 2차 디지털 저역/고역 통과필터 (18) | 2017.01.06 |
| [필터연재] 1차 디지털 저역/고역 통과필터 (17) | 2017.01.05 |