[필터연재] 2차 디지털 저역/고역 통과필터

1차 저역/고역 통과필터를 디지털로 구현하는 것에 대해 지난번[바로가기]에 이야기를 했었습니다. 저는 거의 대부분의 잡음 제거용 필터는 1차만 사용을 하게 되더군요. 그런데 지금은 연재~^^이니 또 다음으로 Band Pass와 Band Stop 필터도 다룰거라~ 의미상 2차 저역/고역 통과필터도 다룰려고 합니다.^^

Filter

[필터연재] 1차 디지털 저역/고역 통과필터

Filter

[필터연재] 2차 디지털 저역/고역 통과필터

Filter

[필터연재] 2차 디지털 Band Pass, Band Stop 필터

일단...

Cut-off 차단 주파수를 결정했다고 하면~

각 주파수를 계산하게 되죠^^

2차는 공진(resonant point)점이 있기 때문에 그 부분을 조절하는 Quality Factor라는 것을 사용합니다. 2차 시스템[바로가기]에서 사용하는 zeta의 역수로 되어 있습니다.

위 식이 2차 저역통과필터의 s-domain에서의 함수입니다.

위 식은 고역통과필터이구요. 두 식이 닮았죠^^.

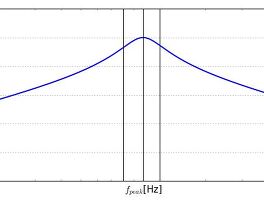
일단 위 그래프는 같은 2차의 저역/고역 통과필터인데 zeta의 변화에 대한 결과를 보여드리는 겁니다. zeta가 낮을 수록 즉, Q가 높을 수록 차단주파수에서 위로 볼록해집니다. 차단 주파수 대역의 신호를 만나면 증폭(공진)될 수 있겠네요. 또 Phase에서는 zeta가 낮을 수록 가파르게 꺾이게 됩니다.

H0 = 1
zeta = 1

Q = 1/2/zeta

num_L2 = np.array([H0*w_cut**2])
den_L2 = np.array([1, w_cut/Q, w_cut**2])
s_L2 = sig.lti(num_L2, den_L2)
w_L2, m_L2, P_L2 = sig.bode(s_L2)

num_H2 = np.array([H0, 0, 0])
den_H2 = np.array([1, w_cut/Q, w_cut**2])
s_H2 = sig.lti(num_H2, den_H2)
w_H2, m_H2, P_H2 = sig.bode(s_H2)

zeta = 0.1
Q = 1/2/zeta
den_2 = np.array([1, w_cut/Q, w_cut**2])

s_L21 = sig.lti(num_L2, den_2)
w_L21, m_L21, P_L21 = sig.bode(s_L21)
s_H21 = sig.lti(num_H2, den_2)
w_H21, m_H21, P_H21 = sig.bode(s_H21)

plt.semilogx(toHz(w_L2), m_L2, lw=2, label='2nd LPF $\zeta =1$')
plt.semilogx(toHz(w_H2), m_H2, lw=2, label='2nd HPF $\zeta =1$')
plt.semilogx(toHz(w_L21), m_L21, lw=1, ls='dashed', label='2nd LPF $\zeta =0.1$')
plt.semilogx(toHz(w_H21), m_H21, lw=1, ls='dashed', label='2nd HPF $\zeta =0.1$')
plt.axvline(f_cut, color='k', lw=1)
plt.xlim(50, 15000)
plt.ylim(-50, 20)
plt.ylabel('Amplitude [dB]')
plt.xticks([100, 1000, 10000], ('','$f_{cut}$[Hz]',''), fontsize = 20)
plt.legend()
plt.grid()

plt.figure(figsize=(12,5))
plt.semilogx(toHz(w_L2), P_L2, lw=2, label='2nd LPF $\zeta =1$')
plt.semilogx(toHz(w_H2), P_H2, lw=2, label='2nd HPF $\zeta =1$')
plt.semilogx(toHz(w_L21), P_L21, lw=1, ls='dashed', label='2nd LPF $\zeta =0.1$')
plt.semilogx(toHz(w_H21), P_H21, lw=1, ls='dashed', label='2nd HPF $\zeta =0.1$')
plt.axvline(f_cut, color='k', lw=1)
plt.xlim(50, 15000)
plt.ylabel('Phase [degree]')
plt.legend()
plt.xticks([100, 1000, 10000], ('','$f_{cut}$[Hz]',''), fontsize = 20)
plt.grid()

plt.show()

위 그림은 zeta를 1로 고정하고, 같은 차단 주파수에서 1차 저역/고역 통과필터와 비교해본 것입니다. 이득에서는 2차계 필터가 좀 더 가파르게 낮아지기 때문에 차단하고자하는 대역의 주파수 성분의 값이 빨리 사라질 것입니다. phase에서는 1차는 0에서 -90 혹은 90에서 0으로 움직인다면, 2차계 필터는 0에서 -180, 혹은 180에서 0으로 움직이게 됩니다.

num_L1 = np.array([w_cut])
den_L1 = np.array([1., w_cut])
s_L1 = sig.lti(num_L1, den_L1)
w_L1, m_L1, P_L1 = sig.bode(s_L1)

num_H1 = np.array([1., 0.])
den_H1 = np.array([1., w_cut])
s_H1 = sig.lti(num_H1, den_H1)
w_H1, m_H1, P_H1 = sig.bode(s_H1)

H0 = 1
zeta = 1

Q = 1/2/zeta

num_L2 = np.array([H0*w_cut**2])
den_L2 = np.array([1, w_cut/Q, w_cut**2])
s_L2 = sig.lti(num_L2, den_L2)
w_L2, m_L2, P_L2 = sig.bode(s_L2)

num_H2 = np.array([H0, 0, 0])
den_H2 = np.array([1, w_cut/Q, w_cut**2])
s_H2 = sig.lti(num_H2, den_H2)
w_H2, m_H2, P_H2 = sig.bode(s_H2)

plt.figure(figsize=(12,5))
plt.semilogx(toHz(w_L2), m_L2, lw=2, label='2nd LPF')
plt.semilogx(toHz(w_H2), m_H2, lw=2, label='2nd HPF')
plt.semilogx(toHz(w_L1), m_L1, lw=1, ls='dashed', label='1st LPF')
plt.semilogx(toHz(w_H1), m_H1, lw=1, ls='dashed', label='1st HPF')
plt.axvline(f_cut, color='k', lw=1)
plt.xlim(50, 15000)
plt.ylim(-50, 20)
plt.ylabel('Amplitude [dB]')
plt.xticks([100, 1000, 10000], ('','$f_{cut}$[Hz]',''), fontsize = 20)
plt.legend()
plt.grid()

plt.figure(figsize=(12,5))
plt.semilogx(toHz(w_L2), P_L2, lw=2, label='2nd LPF')
plt.semilogx(toHz(w_H2), P_H2, lw=2, label='2nd HPF')
plt.semilogx(toHz(w_L1), P_L1, lw=1, ls='dashed', label='1st LPF')
plt.semilogx(toHz(w_H1), P_H1, lw=1, ls='dashed', label='1st HPF')
plt.axvline(f_cut, color='k', lw=1)
plt.xlim(50, 15000)
plt.ylabel('Phase [degree]')
plt.legend()
plt.xticks([100, 1000, 10000], ('','$f_{cut}$[Hz]',''), fontsize = 20)
plt.grid()

plt.show()

이제 s-domain에서 알려진 필터를 디지털 영역인 z-domain으로 데리고 오는 것을 고민해야죠... 뭐 그러나~~~ 이미 교과서(^^)에 있습니다.^^. 

이름은 Bilinear Transform[바로가기]이라고 하구요. 위 식을 변환식으로 사용하면 됩니다.

그러면 2차 저역통과필터의 z-domain에서의 표현은 위와 같고,

고역통과필터는 위와 같습니다. 좀 복잡한가요?^^

위 그림과 같은 direct2form의 필터에 사용하기 위해

이런 일반화식에 적용할려고 하면 각 계수들만 알면 되겠죠^^

LPF의 경우는 위의 식이 될 것이고~

HPF의 경우는 위의 식이 될 겁니다.^^ 위 두 공식을 이용해서 필터계수를 계산하는 코드는

def get2ndFilterCoeffi(f_cut, ts, H0, zeta, isLPF):
    from numpy import pi
    
    w0 = 2*pi*f_cut
    T = ts
    Q = 1/2/zeta
    
    a0_ = 4/T**2 + 2*w0/Q/T + w0**2
    a1_ = -8/T**2 + 2*w0**2
    a2_ = 4/T**2 - 2*w0/Q/T + w0**2
        
    if isLPF=='LPF':
        b0_ = w0**2*H0
        b1_ = 2*w0**2*H0
        b2_ = H0*w0**2
        
    if isLPF=='HPF':
        b0_ = 4*H0/T**2
        b1_ = -8*H0/T**2
        b2_ = 4*H0/T**2
        
    return a1_/a0_, a2_/a0_, b0_/a0_, b1_/a0_, b2_/a0_

로 구현할 수 있겠죠... a0는 어차피 1로 만들거라 위와 같이 하면 되겠습니다. 이제 지난번에도 사용했던 시험신호를 가지고 오면~~

요랬습니다.^^ 이 신호는

이런 주파수 특성을 가지게 만들었죠^^

# Create Test Signal
Fs = 10*10**3               # 10kHz
Ts = 1/Fs                   # sample Time
endTime = 1
t = np.arange(0.0, endTime, Ts)

inputSig = 3.*np.sin(2.*np.pi*t)

sampleFreq = np.arange(10,500,50)

for freq in sampleFreq:
    inputSig = inputSig + 2*np.sin(2*np.pi*freq*t)
    
plt.figure(figsize=(12,5))
plt.plot(t, inputSig)
plt.xlabel('Time(s)')
plt.title('Test Signal in Continuous')
plt.grid(True)
plt.show()

draw_FFT_Graph(inputSig, Fs, title='inputSig', xlim=(0, 600))

a1, a2, b0, b1, b2 = get2ndFilterCoeffi(200, Ts, 1, 1, 'LPF')
dataLPF2 = d2f_2nd(inputSig, a1, a2, b0, b1, b2 )
draw_FFT_Graph(dataLPF2, Fs, title='data_2ndLPF', xlim=(0, 600))

위 코드를 사용해서 2차 저역통과필터를 차단주파수 200Hz에서 설정해서 FFT 결과를 보면

이렇습니다. 이 결과는 아래 1차와 비교하면...

이렇게 됩니다. 1차때와 비교하면 좀 더 가빠르게 신호들을 제거해 갔다는 것을 알 수 있죠....

원신호와 1차 LPF, 2차 LPF를 보면 결과를 비교해볼 수 있습니다. 같은 설정에서 HPF를

a1, a2, b0, b1, b2 = get2ndFilterCoeffi(200, Ts, 1, 1, 'HPF')
dataHPF2 = d2f_2nd(inputSig, a1, a2, b0, b1, b2 )
draw_FFT_Graph(dataHPF2, Fs, title='data_2ndLPF', xlim=(0, 600))

설정해서 결과를 보면...

이렇게 만들어지고~~

Time domain에서 보면.. 1차와의 차이가 보이실 겁니다.^^ 오늘 다룬 코드도 Github[바로가기]에 전체 코드가 공개되어 있습니다.