ROS에서 주행로봇을 움직이게 하는 유명한~ 토픽(topic)은 바로 cmd_vel입니다. 그 이름에서도 나타나 있지만, velocity 속도 명령입니다. 주행로봇을 만약 내가 원하는 어떤 지점으로 보내고 싶다면 보통 많이 하는 절차는 SLAM을 이용해서 지도를 만들고, 그 속에서 amcl 패키지로 맵 안에서 로봇의 위치를 추정하고, move_base를 이용해서 이동 명령을 주게 됩니다.
[Theory/Lecture] - ROS move_base를 이용한 주행 - python 편 -
ROS move_base를 이용한 주행 - python 편 -
최근에 저는 국민대학교에서 주행로봇을 이용해서 겨울방학 특강을 진행했었는데요. 그리고 그 강의가 원격으로 진행되다 보니 수강하는 학생들에게 부족한 부분을 보완하기 위해 영상을 유투
pinkwink.kr
그 내용은 위 글에서 다루었습니다. 그런데 맵위에서 위치를 추정하고 그것을 기반으로 움직이는 거창(^^)한 상황이 아니라, 그냥 단순히, 로봇을 뭐 예를 들어 1m 앞으로 가게, 혹은 1m 앞으로 가면서 살짝 한 20cm 정도 왼족으로 가게, 즉 곡선으로 주행하게, 혹은 몇 도 정도 제자리에서 회전하게 하고 싶을 때도 있습니다.
물론 대부분은 cmd_vel 명령으로 대부분 소화하는 상황이 더 많겠지만, 아주 가끔은 방금 위에서 제가 이야기한대로 짧은 거리, 위치 명령을 이수하게 하고 싶을때도 있을 수 있습니다. 저도 최근 그런 명령이 필요했는데요. 희한하게 누가 ROS 패키지로 만들어 놨을것~ 같은데 없더라구요. 뭐 못 찾았을 수도 있죠. 아무튼 그렇다고 마냥 검색만 하고 있을 수는 없으니 만들어야겠다~ 생각하고 만들기 시작했습니다. 미리 오늘 이야기할 코드의 한계를 이야기 합니다. 즉 제가 쓸려고 만들었으니, 저만 만족하면 되는거라 한계가 당연히 있는거죠^^. 미리 그 한계를 이야기하고 진행하겠습니다.
- 조금 큰 로봇이면서 로봇 자체가 바퀴의 회전 각도 측정에 오차가 있는 로봇을 대상으로 만들어서 주행거리와 각도의 허용 오차가 조금 있습니다.
- 원래 의도는 목표지점까지 갈때 그 방향으로 제자리 회전을 한 후에 출발하는 시나리오를 생각하고 만들었습니다.
- 그러나 완전히 오차없이 제자리 회전을 완료하지 못할 확률이 높으니 도착 목표지점이 조금 옆에 있어도 이동을 완료할 수 있도록 주행 명령도 x, y 좌표를 목표로 움직이도록 합니다.
- 뒤로 가는 기능은 아름답게 구현되어 있지 않습니다. 위의 이유로 가고자 하는 방향으로 먼저 제자리 회전을 하도록 할 예정이기 때문입니다.
- 그리고 한 번 이동을 완료하면 로봇의 odom 계산을 reset합니다. 그건 odom은 오차가 생길 수 밖에 없어서 주행을 계속하면 누적 오차가 만만치 않기도 하고, 제가 사용할 목적은 한 지점, 한 지점 계속 이동하는거라 그냥 이렇게 만들어 두었습니다.
간단한 이론적 배경
그럼 일단, 간단한 이론적인 이야기도 해야겠네요^^ 아래 그림과 수식은 모두 간단한 한 논문의 내용을 참조했습니다. 보통 일반적인 내용이기도 합니다.

먼저 로봇이 가고자 하는 위치는 (x_ref, y_ref) 입니다. 현재 로봇은 theta의 방향으로 회전 중에 있구요. 이럴때 로봇에게 얼마만큼의 직진 명령과 얼마만큼의 회전명령, 즉 cmd_vel을 얼마나 주면 도착할 것인가? 하는 문제에 대한 이야기입니다. cmd_vel의 구성은 직진 성분의 속도 명령과 회전 성분의 속도 명령이 있으므로 우리도 직진 성분과 회전 성분의 명령을 만들면 되겠습니다. 결국 그 명령을 만들기 위해서는 직진 성분의 현시점 에러와 회전에 대한 현시점 에러를 계산할 수 있으면 간단히 PID 제어기를 꾸며서 진행할 수 있을 것 같네요.

일단 각도에 대한 에러는 매우 간단한 편입니다. 먼저 현 지점(x, y)에서 목표 지점(x_ref, y_ref)의 값에 간단히 삼각함수를 적용하면 theta_ref를 구할 수 있습니다. 그리고 현재 각도 theta와의 차이를 이용하면 각도의 에러인 e_theta를 계산할 수 있습니다.
그 다음 직선 성분에 대한 에러 e_s인데요. 이건 조금 애매할 수 있지만, 로봇 진행 방향의 R 지점까지의 거리를 e_s로 보겠습니다. 어차피 각도의 에러를 0으로 만들다 보면 목표 지점 (x_ref, y_ref)가 R과 같아지기를 기대하는 거죠. 오차가 있을 수 있지만, 제가 사용하는데는 큰 무리가 없어서 그냥 그렇게 사용하도록 하겠습니다. R 지점까지의 거리는 역시나~ 삼각함수를 이용해서 구할 수 있습니다. 이 부분에 대한 해설은 글로는 조금 힘들어서 이 글 마지막에 연결해 놓을 동영상에서 간략히 설명을 더 해보도록 하겠습니다.
def calc_errors(cur_pos, goal):
delta_y_ref = goal.y - cur_pos.y
delta_x_ref = goal.x - cur_pos.x
if ((goal.x == 0.) and (goal.y == 0.)):
e_s = 0.
else:
goal.theta = atan2(delta_y_ref, delta_x_ref)
e_s = sqrt(delta_x_ref**2 + delta_y_ref**2) * cos( atan2(delta_y_ref, delta_x_ref) - cur_pos.theta )
e_theta = goal.theta - cur_pos.theta
return e_s, e_theta위 코드는 각도와 거리의 에러를 계산하는 수식에 맞춰 코드로 만들어 둔 것입니다. 그 중에 목표지점의 좌표가 0, 0으로 들어오면 제자리 회전이라고 생각하도록 처리해 두는 부분이 조건문(if)에 있습니다.

이제 전체 컨트롤러의 구성은 위 그림처럼 해 두겠습니다. 방금 e_s, theta_ref를 각각 계산하고 다시 e_theta를 계산하는 부분을 만들고, 이제 Controller를 만들어야 합니다. 컨트롤러는 간단히 class로 별도로 만들어 두도록 하죠
#!/usr/bin/env python
import rospy
class RobotState(object):
x = 0.0
y = 0.0
theta = 0.0
class PID:
def __init__(self):
self.P = 0.0
self.I = 0.0
self.D = 0.0
self.max_state = 0.0
self.min_state = 0.0
self.pre_state = 0.0
self.dt = 0.0
self.integrated_state = 0.0
self.pre_time = rospy.Time.now()
def process(self, state):
dt = rospy.Time.now() - self.pre_time
if self.dt == 0.:
state_D = 0.
else:
state_D = (state - self.pre_state) / self.dt
state_I = state + self.integrated_state
out = self.P*state + self.D*state_D + self.I*state_I * self.dt
if out > self.max_state:
out = self.max_state
elif out < self.min_state:
out = self.min_state
self.pre_state = state
self.integrated_state = state_I
self.pre_time = rospy.Time.now()
return out위 코드를 저장해 두고 필요할 때
while True:
e_s, e_theta = calc_errors(cur_pos, goal)
speed.angular.z = theta_PID.process(e_theta)
speed.linear.x = translation_PID.process(e_s)
pub.publish(speed)이렇게 에러를 계산하고 회전방향과 직진방향의 제어 입력을 각각 계산하도록 만들고 ROS cmd_vel 토픽에 발행하도록 연결해버리면 그만입니다.
코드 설명과 패키지 사용법
이제 이 과정은 모두 actionlib으로 만들어 둘 예정입니다. 해당 코드는 OMO R1mini의 ROS melodic 버전 패키지에 포함시켜 두었습니다. 방문해 보시면 지금 이 글에서 다루는 부분은 다 보실 수 있습니다. 지금부터는 해당 패키지를 소개하고 사용하는 방법에 대해 이야기를 하겠습니다.

먼저 이 코드는 로봇의 움직임을 약간 상위 레벨에서 다루기 편한 도구가 단한히 topic보다는 actionlib이 좋더군요. move_base도 그렇게 되어 있구요. 그래서 저도 그렇게 만들기로 했습니다. 그러니 당연히 VanillaPosition.action 파일을 정의해 둔것이죠. 액션 definition 파일은 goal, result, feedback으로 구성되어야 합니다.

그리고 PID 제어기에서 사용할 PID 게인과 언제 제어기를 끝낼지 조건을 지정하는 설정까지를 controller_setting.yaml에 저장해 두었습니다.
www.youtube.com/watch?v=kq2F1SeLQ1I&list=PL83j7f4UkozHPUshNQfPpogJBE0gSnCYH&index=11
오늘 글에서는 ROBOT은 OMO R1mini입니다. 혹시 OMO R1mini의 ROS 관련 기능을 학습하고 싶으시다면 위 동영상부터 해당 재생목록을 열람하시면 됩니다.
pinkwink.kr/1318?category=709117
Jetson Nano나 라즈베리파이로 VSCODE로 SSH 접근하기
젯슨 나노나 라즈베리파이와 같은 소형 싱글보드컴퓨터(SBC)를 사용할때 원격으로 접속을 많이 하실겁니다. 주로 ssh를 많이들 이용하시겠죠. 그런데 이 ssh로 접근을 하면 다른 건 괜찮은데 코드
pinkwink.kr
그리고 이번 글은 OMO R1mini라는 로봇에 원격으로 접속해서 ROS를 실행하고 VSCODE로 실행할 거라 혹시 VSCODE를 이용해서 원격으로 로봇에 접근하는 법이 궁금하시다면 위의 글을 읽고 오시면 됩니다.
이제 VSCODE에서
터미널을 열고 bringup을 실행합니다. 보통 주행로봇들은 대부분 bringup 패키지가 있을거에요. 그리고 그 패키지들은 로봇을 직접 구동하고 odom을 발행하는 일을 해줄겁니다. 혹시 확인하고 싶다면

또 다른 터미널을 열고 rostopic list를 확인하면 됩니다. cmd_vel과 odom만 있다면 됩니다. 이제 github에서 확인할 수 있는 해당 패키지를 실행하면 됩니다.

저 패키지를 실행한 후에,

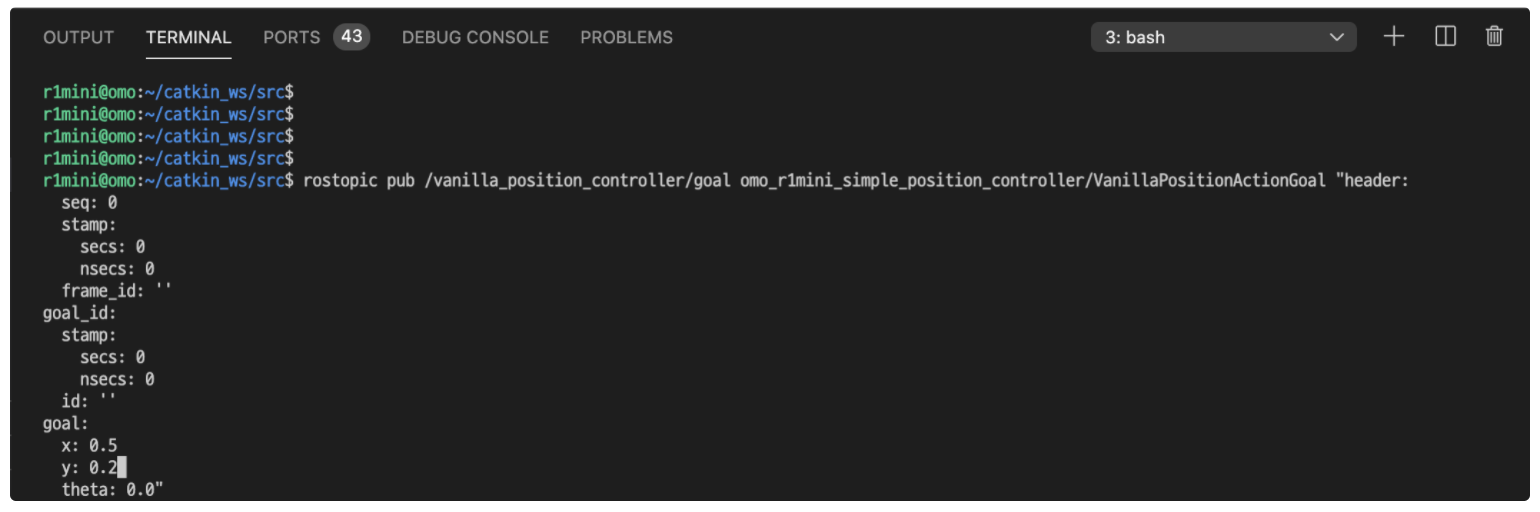
rostopic list를 확인해보면 관련된 topic이 추가된 것을 확인할 수 있습니다. 저기서 /vanilla_position_controller/goal 토픽으로 목표 좌표를 쏴주면(^^) 됩니다.

위 그림처럼 토픽을 발행 pub 하면 됩니다. 탭키를 적극적으로 활용하세요. 그러면 거의 다 완성됩니다. 그리고 화살표키로 살짝 옆으로 가서 몇 가지 숫자만 수정하면 되죠.

네, 저렇게 x, y는 0을 주고, theta만 값을 (라디안 단위로) 주면 회전을 합니다.

그러면 위 그림처럼 로봇이 제자리 회전을 시작합니다. 그러나 눈으로 볼때는 약간 오차가 있을 수 있습니다. 대략 2도 정도 범위에 들어가면 멈추도록 조건이 되어 있기도 하고, 저렇게 기어박스를 작착한 로봇들은 기어 유격으로 모터기준으로는 오차가 허용한 범위내에 들어갔을 수 있지만, 실제 눈으로 볼때는 오차가 있을 수 있습니다.

그리고 로봇이 출발할때는 빨간색 화살표의 방향을 보면서 있었는데 지령을 0.5, 0.2 정도로 주면 파란색 화살표가 가르키는 지점으로 곡선으로 주행을 하게 됩니다.
지령은 위 그림처럼 준거죠.

그러면 패키지가 실행되는 터미널을 보면 잔여 거리 에러와 각도의 에러 (보기 편하게 degree로 되어 있습니다.)가 나타납니다. 그리고 odom이 리셋된다는 메세지도 함께 나타납니다.
이번글의 내용은 아래 동영상에도 함께 공유됩니다.
'Robot > Robot Program - ROS' 카테고리의 다른 글
| ROS Melodic에서 YOLO로 detection 된 사람 수 세기 (16) | 2022.03.17 |
|---|---|
| ROS 카메라 캘리브레이션 수행하기 (12) | 2021.04.27 |
| ROS 토픽을 터미널에서 그래픽하게 보여주는 rosshow (2) | 2021.03.21 |
| Ubuntu 20.04에서 ROS1 Noetic과 ROS2 Foxy 같이 설치하기 (12) | 2021.02.22 |
| Noetic에서 catkin tools 설치 및 alias 설정 (8) | 2021.02.16 |
| SSH로 접근할때 remote identification 에러 대응 (2) | 2021.02.01 |
| 라즈베리파이의 라즈비안에 ROS melodic 버전에서 YDLIDAR 설치하기 (6) | 2021.01.29 |



