저는 취미처럼 요즘 기구학을 학습해가고 있는데요. 사실 제가 기구학에 관심을 가진건 예전.. 음 그러니까 제가 첫 직장을 관두고[바로가기], 여기저기 밥 얻어먹고 다니던(^^) 시절에 로보링크에 한 이사님이 선물해 주신 로봇 교육용 키트로 만든 로봇암[바로가기] 때문인데요.^^. 이걸가지고 뭐 재미나게 놀게 없을까 하다가 시작된 것이지요. 물론 지금의 회사일을 볼때 조금 있다가 사용될 지식이기도 합니다만... 지금은 모터제어기(보다는 약간 로봇제어기에 가까운)에 집중하고 있기 때문에 당장 사용될 건 아닙니다만^^. 뭐 아무튼 그렇다는 거죠^^ 그래서 처음에 예제로 Two Link Planar를 대상으로해서 MATLAB으로 검증하면서 기초적인 부분을 확립하면서 정기구학을 했고[바로가기], 그 후 Processing을 이용해서 약간 더 괜찮아 보이는 화면으로 시뮬레이션을 진행했죠.[바로가기] 이제 정 기구학을 다루던 Two Link Planar라는 간단한 예제를 했으니 이번에는 동일 예제를 가지고 역기구학 이야기를 해볼까 합니다.~~^^ 여기서 잠시 정 기구학은 각 관절의 상태(각도나 이동 거리 등)를 알고 있어서 끝단의 정보를 계산할 때, 역 기구학은 원하는 끝단의 정보(위치나 속도)를 가지고 각 관절의 상태를 결정하는 것입니다.^^
위 그림은 지난번에도 출처를 찾지 못 했다는 아무튼 그 Two Link Planar입니다. 지난번 글[바로가기]에서 결론을 낸 식을 다시 가져다 오면
이었죠. 좌변과 우변을 적절히 전개해서 theta1, theta2를 얻어내는 것이 이번 예제의 역기구학의 목표가 됩니다.~~
일단 우변의 최 좌측행렬인 z축 중심으로 theta1만큼 회전하는 행렬을 우변에서 소거할 건데요. 당시에도 이야기했지만, 회전행렬의 역행렬은 그냥 전치(transpose) 행렬과 같습니다.~^^
이제 그 역행렬을 양변에다가 곱하고, 전개하고, 또 살짝 정리하면
요렇게 되지요~~~^^. 아 이걸 손으로 다 전개했냐구요??? 음 뭐 사실.. 저걸 손으로 다 전개해서 정리를 하고 그걸 다시 쳐다보면 뭔가 뿌듯함도 느껴지고 일종의 쾌감도 있지만... 지금은 회사생활때문에 낮에 못하고, 집에오면 또 맞벌이 부부의 비애로 집안일을 거들어야하기 때문에 한가롭게 저걸 전개할 시간이 없죠~~^^ 이럴때 정~말 편리한 도구가 하나 있습니다. [바로가기]와 [바로가기], [바로가기]에서 다룬 MATLAB의 문자 연산을 이용해서 전개하면 아~주 쉽답니다.~~^^
syms th1 th2 nx ny nz ox oy oz ax ay az Px Py Pz a1 a2 RotZ1 = [cos(th1) -sin(th1) 0 0; sin(th1) cos(th1) 0 0; 0 0 1 0; 0 0 0 1] RotZ2 = [cos(th2) -sin(th2) 0 0; sin(th2) cos(th2) 0 0; 0 0 1 0; 0 0 0 1] TransA1 = [1 0 0 a1; 0 1 0 0; 0 0 1 0; 0 0 0 1] TransA2 = [1 0 0 a2; 0 1 0 0; 0 0 1 0; 0 0 0 1] T_0_2 = RotZ1*TransA1*RotZ2*TransA2 TT = [nx ox ax Px; ny oy ay Py; nz oz az Pz; 0 0 0 1] % Left Step 1 LS1 = simplify(inv(RotZ1)*TT) % Right Step 1 RS1 = simplify(inv(RotZ1)*T_0_2)
위 MATLAB 코드는 기구학적 계산을 문자연산으로 수행하고 있습니다. 자세한 사용법은 방금 이야기한 이전에 문자연산을 이야기한 글로 넘기고, 그 결과는 좌변과 우변을 각각 표현해서 보면
와 같은 결과를 얻을 수 있습니다. 이걸 정리해서 보면~~ 아까 위의 식이 되는 거죠~~!^^ 아무튼 그 식에서 좌/우변의 (1,4)와 (2,4)번 요소를 비교하면
입니다. 이 두식을 모두 양변 제곱 후에 더해서 정리하면
를 얻을 수 있습니다. 여기서
라는 삼각함수 공식을 적용하면
이 됩니다. 여기서 +-기호가 모두 있네요. 맞습니다. 역기구학은 실제로 구해보면 해가 하나가 아닐때가 더 많습니다. 사실 해가 하나만 있는 경우가 드물더군요.ㅠㅠ. 실제 로봇에 적용할때는..ㅠㅠ. 뭐 아무튼... theta2를 일단 알게 되었습니다.
다시 아까 원래 그림에서 각 psi를 정의합니다. 이 걸 이용하면
tan psi를 표현할 수 있게 되고,
또 위 식을 이용해서 theta1을
이렇게 얻을 수 있습니다. 아참.. 표현은 위와 같이 했지만, 우변의 첫 번째 tan의 역함수는 일반적으로 대부분의 언어에서 지원하는 atan2를 사용할 겁니다. 아무튼 이렇게 되면 Px, Py라는 최종단 좌표가 정해지면 방금 쭈~욱 전개해서 구한 theta1/theta2를 알 수 있게 되는 것입니다. 이게 역기구학의 목적인것이지요~~^^ 그걸 구하는 과정을 MATLAB으로 보면
Px = -20; Py = 15; th2 = [2*atan((((a1+a2)^2-(Px^2+Py^2))/(Px^2+Py^2-(a1-a2)^2))^0.5) -2*atan((((a1+a2)^2-(Px^2+Py^2))/(Px^2+Py^2-(a1-a2)^2))^0.5)] th1 = atan2(Py,Px) - atan(a2*sin(th2)./(a1+a2*cos(th2)))
입니다. 별거 없이 위에서 구한 식을 그냥 적용했을 뿐이지요~~^^ 그러면 이전에 MATLAB에서 정방향 기구학을 이야기했던 그 코드를 바로 사용할 수 있습니다.
syms th1 th2 nx ny nz ox oy oz ax ay az Px Py Pz a1 a2 RotZ1 = [cos(th1) -sin(th1) 0 0; sin(th1) cos(th1) 0 0; 0 0 1 0; 0 0 0 1] RotZ2 = [cos(th2) -sin(th2) 0 0; sin(th2) cos(th2) 0 0; 0 0 1 0; 0 0 0 1] TransA1 = [1 0 0 a1; 0 1 0 0; 0 0 1 0; 0 0 0 1] TransA2 = [1 0 0 a2; 0 1 0 0; 0 0 1 0; 0 0 0 1] T_0_2 = RotZ1*TransA1*RotZ2*TransA2 TT = [nx ox ax Px; ny oy ay Py; nz oz az Pz; 0 0 0 1] % Left Step 1 LS1 = simplify(inv(RotZ1)*TT) % Right Step 1 RS1 = simplify(inv(RotZ1)*T_0_2) %% a1 = 15; a2 = 15; Px = -20; Py = 15; th2 = [2*atan((((a1+a2)^2-(Px^2+Py^2))/(Px^2+Py^2-(a1-a2)^2))^0.5) -2*atan((((a1+a2)^2-(Px^2+Py^2))/(Px^2+Py^2-(a1-a2)^2))^0.5)] th1 = atan2(Py,Px) - atan(a2*sin(th2)./(a1+a2*cos(th2))) %% % DH Table % | theta d a alpha % --------------------------------- % 1 | theta1 0 a1 0 % 2 | theta2 0 a2 0 RotZ = @(theta) [cos(theta) -sin(theta) 0 0; sin(theta) cos(theta) 0 0; 0 0 1 0 ; 0 0 0 1]; Trans = @(x, y, z) [1 0 0 x; 0 1 0 y; 0 0 1 z; 0 0 0 1]; for i=1:2 theta1 = th1(i); theta2 = th2(i); T_0_1 = RotZ(theta1)*Trans(a1, 0, 0); T_1_2 = RotZ(theta2)*Trans(a2, 0, 0); T_total = T_0_1*T_1_2; y0 = [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1]; y0_1 = T_0_1 * y0; y0_2 = T_total * y0; originX = [y0(1,4), y0_1(1,4), y0_2(1,4)]; originY = [y0(2,4), y0_1(2,4), y0_2(2,4)]; figure plot(originX, originY, '*--', 'linewidth', 2); axis([min([originX, originY])-4, max([originX, originY])+4, min([originX, originY])-4, max([originX, originY])+4]) grid on axis square axisY0X = y0(1, 1:2); axisY0_1X = y0_1(1, 1:2); axisY0_2X = y0_2(1, 1:2); axisY0Y = y0(2, 1:2); axisY0_1Y = y0_1(2, 1:2); axisY0_2Y = y0_2(2, 1:2); line([originX(1), axisY0X(1)], [originY(1), axisY0Y(1)], 'color', 'r', 'linewidth', 3); line([originX(1), axisY0X(2)], [originY(1), axisY0Y(2)], 'color', 'g', 'linewidth', 3); line([originX(2), originX(2)+axisY0_1X(1)], [originY(2), originY(2)+axisY0_1Y(1)], 'color', 'r', 'linewidth', 3); line([originX(2), originX(2)+axisY0_1X(2)], [originY(2), originY(2)+axisY0_1Y(2)], 'color', 'g', 'linewidth', 3); line([originX(3), originX(3)+axisY0_2X(1)], [originY(3), originY(3)+axisY0_2Y(1)], 'color', 'r', 'linewidth', 3); line([originX(3), originX(3)+axisY0_2X(2)], [originY(3), originY(3)+axisY0_2Y(2)], 'color', 'g', 'linewidth', 3); xPol = [1, 2, 1, 1]; yPol = [1, 1, 2, 1]; pol0 = [xPol; yPol; [0 0 0 0]; [1 1 1 1]]; pol0_1 = T_0_1*pol0; pol0_2 = T_total*pol0; line(xPol, yPol, 'color', 'k', 'linewidth', 2); line(pol0_1(1,:), pol0_1(2,:), 'color', 'k', 'linewidth', 2); line(pol0_2(1,:), pol0_2(2,:), 'color', 'k', 'linewidth', 2); end
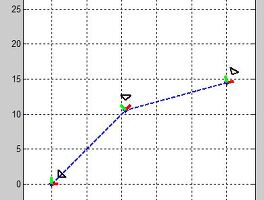
위 코드는 전체 코드입니다. 뭐 별거 아니지만~~^^. 아무튼 이아이는 GitHub에 있으므로 다운로드를 받으실 수 있습니다.^^.[바로가기] 일단 위에서 미리 이야기했듯이 역기구학을 풀면 해가 하나만 나오지 않을 때가 있습니다. 이번 예제는 두 개의 해가 존재하는데요. 이게 어떤걸 선택할 것인가는 역시 사용자가 정해야하는 것으로 보입니다. 아무튼 저걸 실행한 결과를 보면
최종단 위치를 20,15로 했을때 보여주는 두개의 역기구학 해입니다.
최종단 위치를 -20,-15로 했을 때의 결과이구요.
30,0과 0,-30을 각각 최종 위치로 봤을 때의 모습니다. 아무튼 이렇게 또 기본을 익혀 보았네요. 다음은 역기 Processing으로 잘 한 번 만들어 볼까 생각중이랍니다.~~^^ 그나저나 실제 로봇에 적용을 해봐야할 텐데... 뭐 언젠가 그런 시간과 돈(^^)과 마음의 여유가 생기면 그때 하죠 뭐~~~ 어차피 취미생활인데 말이죠~~ ㅋㅋ
'Theory > ControlTheory' 카테고리의 다른 글
| 엑셀에서 저역통과필터 (Low Pass Filter) 구현하기 (48) | 2015.05.12 |
|---|---|
| [DC 모터 제어] DC 모터 동역학 및 전류제어기의 MATLAB을 이용한 시뮬레이션 (44) | 2015.04.14 |
| 모터 제어할 때, 부드러운 위치 프로파일을 위해 사다리꼴 속도 프로파일 생성하기 (22) | 2014.12.26 |
| 정방향 기구학(forward kinematics)의 기초와 Two Link Planar 예제 (22) | 2014.11.14 |
| 델타형 병렬 로봇의 역기구학을 단순 기하학적으로 손쉽게 해석해보기 (10) | 2014.04.25 |
| 저역통과필터와 고역통과필터를 C로 구현 (39) | 2011.06.01 |
| [C/C++] 배열을 사용하지 않고 평균 구하기 (6) | 2011.03.25 |