이번에는 Logistic Regression 로지스틱 회귀이야기를 해보려고 합니다. 이름은 Regression 회귀이지만 실제로는 분류 문제입니다. 먼저 이 글의 이전글이 어떤 내용이었는지부터 시작해보죠.
이전 이야기 선형 회귀 Linear Regression

저 그림으로 지난 글에서 선형회귀 이야기를 마무리했었습니다.
https://pinkwink.kr/1376?category=926564
Cost Function 비용함수와 Gradient Descent 경사하강법의 이해 (feat. tensorflow GradientTape)
아마 딥러닝이 되었든 혹은 간단한 선형 회귀 알고리즘만 공부하려고 해도 비용함수라고 하는 Cost Function(loss funciton)이라고 하는 단어를 만났을 겁니다. 특히 그 후 꼭 따라 붙는 Gradient Descent 경
pinkwink.kr
선형 회귀는 주어진 데이터를 직선으로 표현하려는 것이었습니다.

직선으로 표현하기 위해 일단 가설(혹은 모델)을 직선이라고 두었었구요.
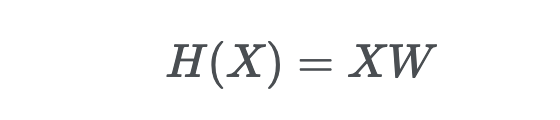
그리고 비용(cost 혹은 loss) 함수를 정의했습니다.
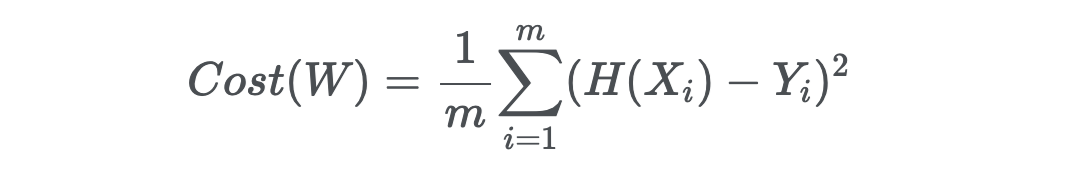
그리고 저 비용함수를 하는 일이 미분해서 가중치를 어떻게 업데이트할 것인지를 결정하는 것이었죠
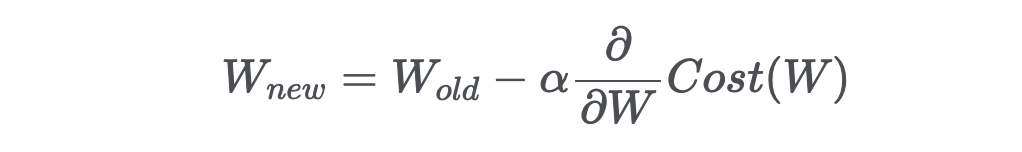
이것은 어떻게 데이터를 직선으로 표현할 것인지를 고민하는 것이었습니다. 그런데 말이죠. 만약에 데이터를 직선으로 표현하는 것이 아니라 직선을 이용해서 데이터를 구분하고 싶다면 어떻게 하죠? 지금까지 이야기한 것은 회귀(regression) 문제라고 합니다.
분류 classification - Logistic Regression
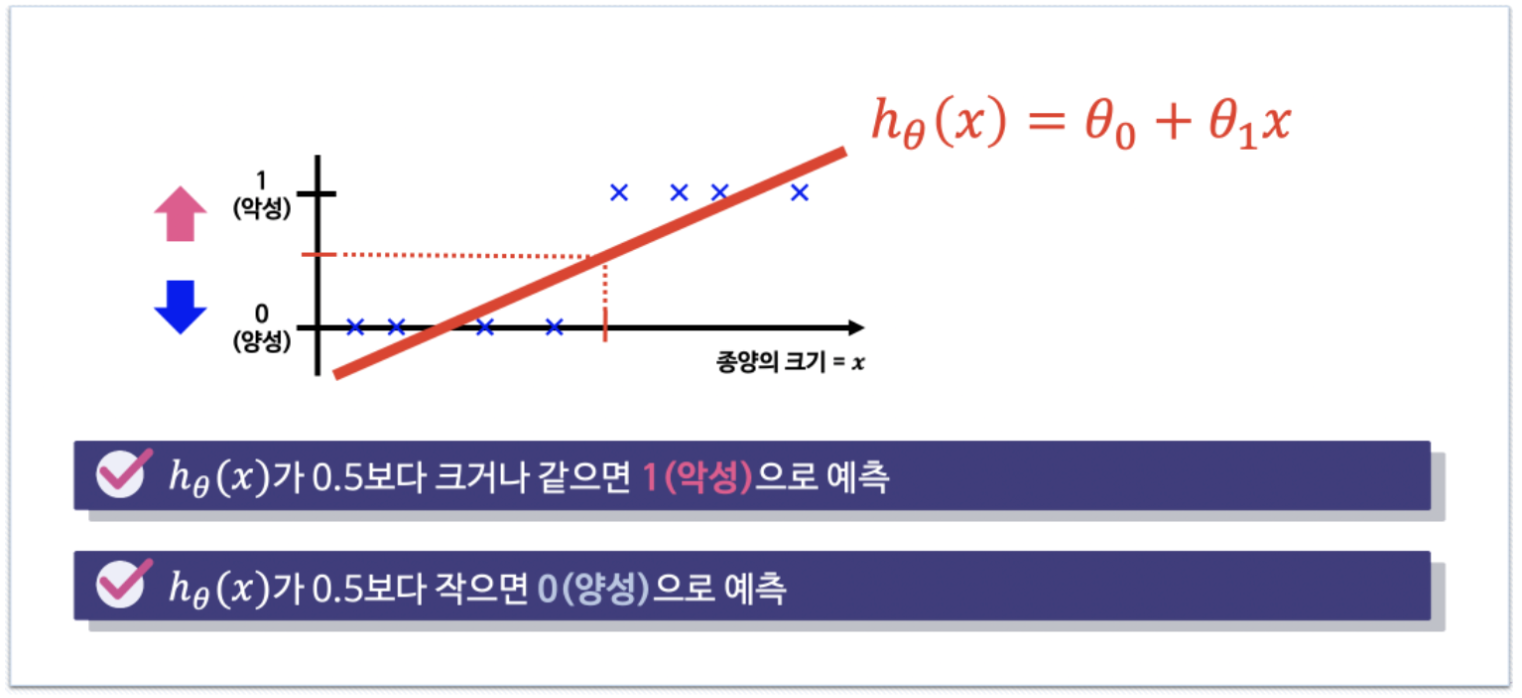
지금 이야기를 하려고 하는 것은 분류(classification) 문제입니다. 종양의 크기를 보고 양성이나 음성이냐를 나누는 문제, 그냥 1과 0을 구분하는 문제로 보는 것을 흔히 이진 분류라고 합니다. 분류는 회귀와 달리 데이터를 분류하는 경계를 찾는 것이라서, 특히 이진 분류는 라벨(정답)이 0 아니면 1입니다.
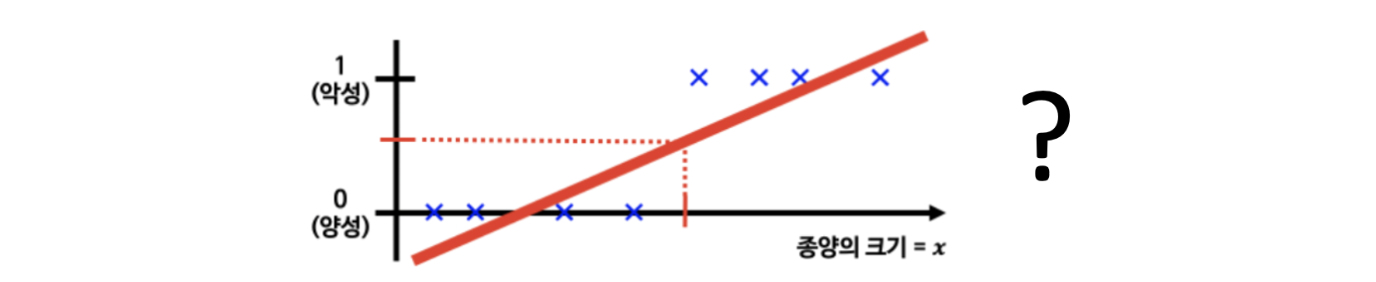
그러니 저렇게 회귀처럼 분류문제를 풀수는 없는거죠. 그래서 조금 특별한 장치가 필요합니다.
분류 문제를 풀기위해 출력을 0과 1사이로 제한할 필요가 있다

네, 우리가 학습에 사용할 데이터의 정답(라벨)은 이진 분류 문제에서는 0과 1입니다. 뭐 모델이 동작하다가 0과 1사이의 값을 준다면 그건 0.5를 기준으로 크면 1, 작으면 0이라고 할 수 있습니다. 결국 학습할 모델의 출력이 어떻게 하면 0과 1 사이의 값을 가지게 할 것인가 인거죠. 그 특별한 장치가 하나 필요합니다.
sigmoid function
그 특별한 장치는 시그모이드 함수입니다.

이렇게 함수는 생겼구요.

이렇게 코드를 이용해서 확인하면

이렇게 생겼습니다. 출력이 0과 1사의 값을 가지는거죠. 그러면 선형회귀의 출력에 다시 시그모이드 함수를 입혀버리면 출력이 0과 1사이의 값이 되도록 만들 수 있는 겁니다.
그럼 비용(cost) 함수는 어떻게 정의하지? - cross entropy
그러면 또 하나의 문제가 생깁니다. 라벨이 0과 1뿐이고 출력은 0과 1사이의 값을 가지는데, 비용함수를 어쩔거냐는 거죠. 라벨이 0일때는 0에 가까울 수록, 라벨이 1일때는 1에 가까울 수록 적은 값을 가지도록하는 비용함수를 만들어야 합니다.
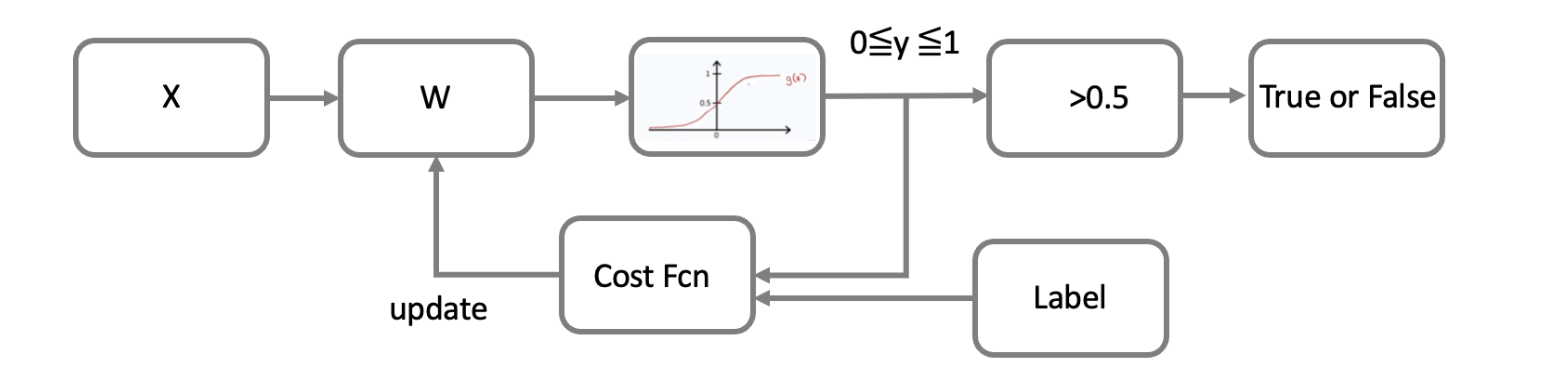
그 역할을 해 줄 수 있는 아이가 바로 cross entropy 입니다.
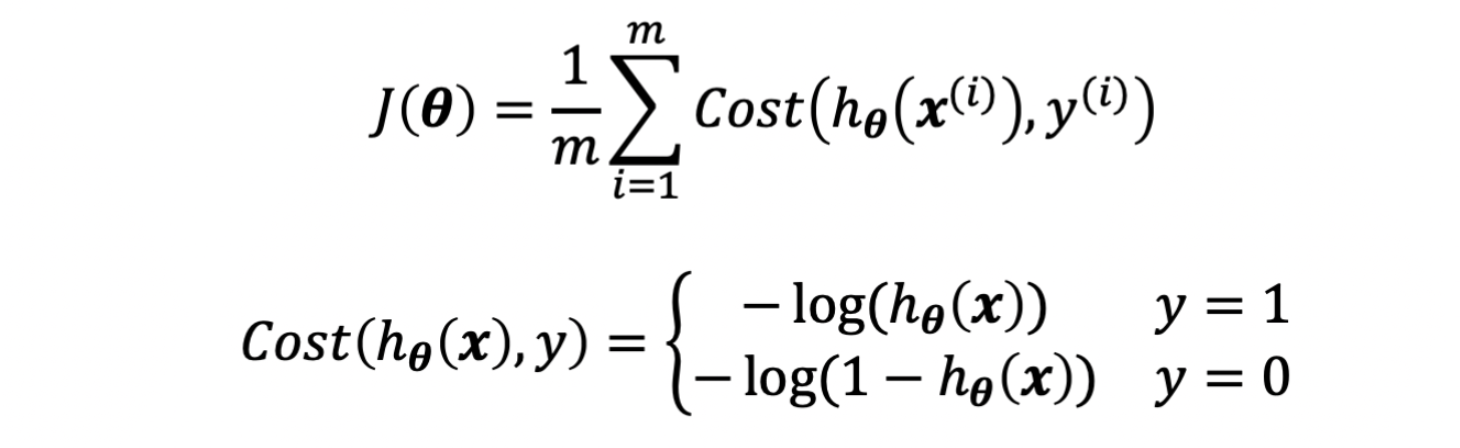
저 수식을 상세히 보면 y(라벨)가 1이냐 0이냐에 따라 각각 다른 함수가 적용됩니다.

위 코드로 살짝 그려보면
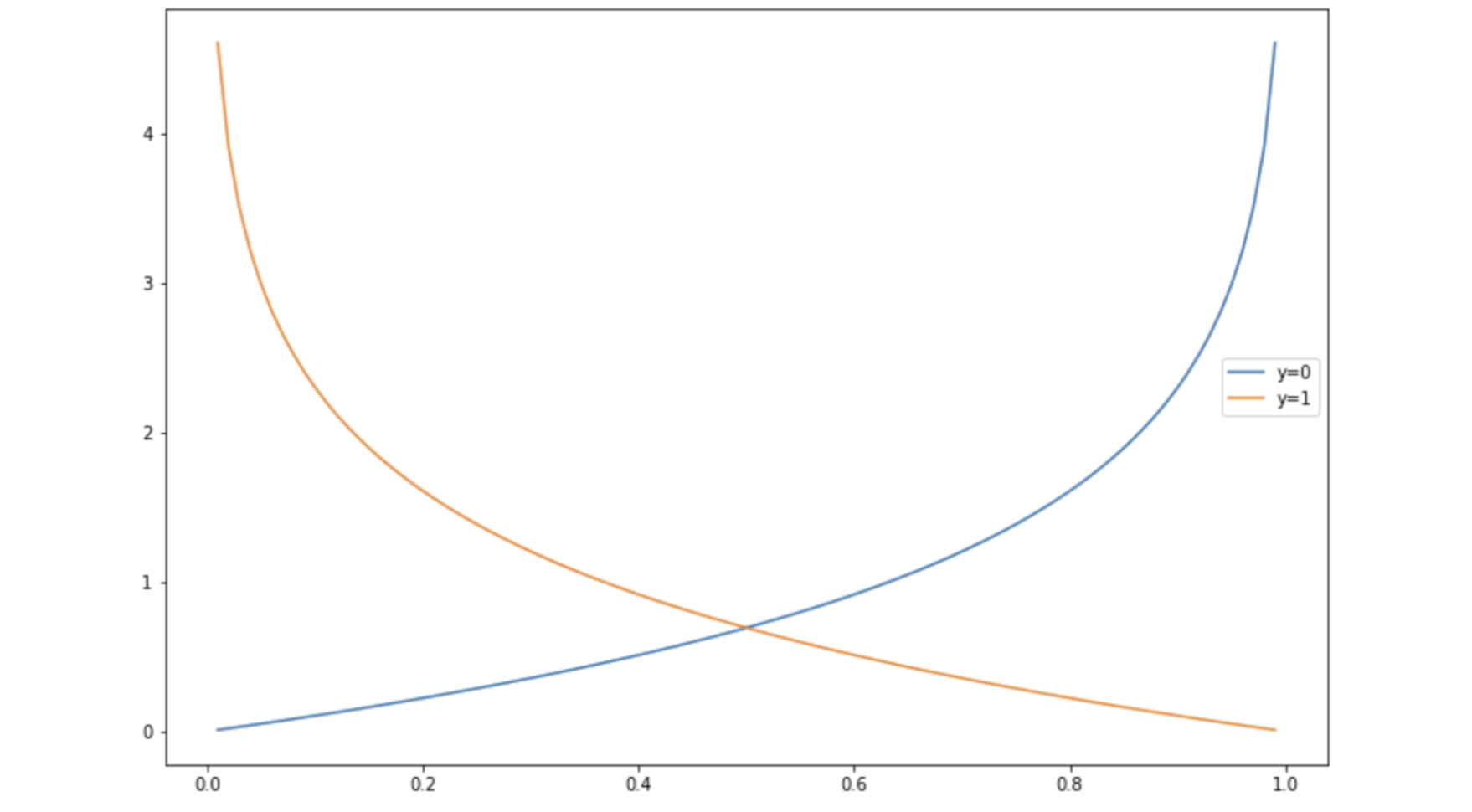
이렇게 되는데요. y가 1일때와 0일때 각각 비용함수의 모양이 다릅니다. 그래서 분류에 대한 학습이 이뤄지는거죠.
코드로 확인해보자~
간단한 데이터를 먼저 준비하겠습니다.
import numpy as np
X = np.array([[1., 1.], [1., 2.], [2., 1.],
[3., 2.], [3., 3.], [2., 3.]], dtype=np.float32)
y = np.array([[0.], [0.], [0.], [1.], [1.], [1.]], dtype=np.float32)어떻게 생겼는지 확인해보면
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
df = pd.DataFrame(X, columns=['x1','x2'])
df['y'] = y
plt.figure(figsize=(6,6))
sns.scatterplot(x='x1', y='x2', hue='y', data=df, s=500)
plt.show()
이렇게 생겼습니다. 저 가운데 대각선 부분을 지나가도록 경계를 만들면 되는 거겠죠?^^
import tensorflow as tf
W = tf.Variable(tf.random.normal([2, 1], mean=0.0))
b = tf.Variable(tf.random.normal([1], mean=0.0))
print("Initial Weight : ", W.numpy())
print("Initial Bias : ", b.numpy())가중치와 바이어스를 만들구요~
def logistic_reg_output(X):
z = tf.matmul(X, W) + b
return 1 / (1 + tf.exp(-z))
def cross_entropy(y_pred, y):
output = tf.reduce_mean(-tf.reduce_sum(y*tf.math.log(y_pred)
+ (1-y)*tf.math.log(1-y_pred)))
return output로지스틱 분류를 하는 함수와 비용함수를 만들어 둡니다.
lr = 0.001
num_iter = 10000
hist_loss = []
hist_W = []
hist_b = []
idx_label = []여러가지 목적으로 변수 몇몇을 초기화하구요
for n in range(num_iter):
with tf.GradientTape() as tape:
y_hat = logistic_reg_output(X)
loss = cross_entropy(y_hat, y)
updated_W, updated_b = tape.gradient(loss, [W, b])
W.assign_sub(lr * updated_W)
b.assign_sub(lr * updated_b)
hist_loss.append(loss.numpy())
if n%200==0:
print(n, '\t', ' : Loss : ', loss.numpy())
hist_W.append(W.numpy())
hist_b.append(b.numpy())
idx_label.append(n)학습을 시작합니다.~
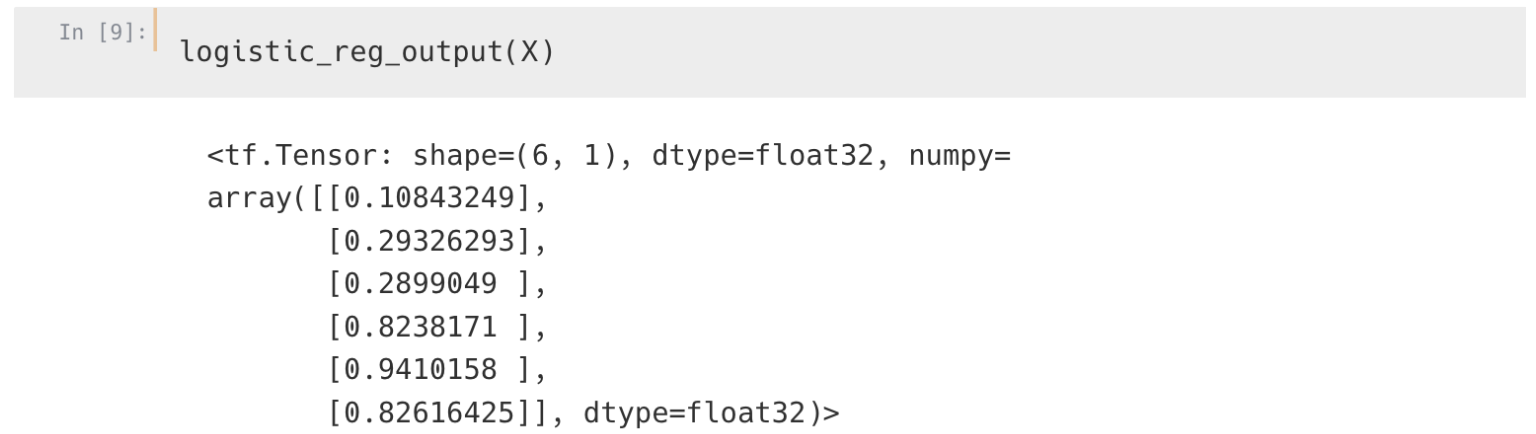
결과는 잘 나온듯 합니다. 0.5 기준으로 0과 1로 잘 구분 되는것 같아요.

loss도 잘 떨어지구요. 좀더 학습시켜도 괜찮을것 같기도 해요.
결정경계 확인을 위한 작업
이번에는 조금 더 확인을 위해
xv = np.arange(0., 3.5, 0.1, dtype=np.float32)
yv = np.arange(0., 3.5, 0.1, dtype=np.float32)
xx, yy = np.meshgrid(xv, yv)
X_draw = xx.reshape(-1,)
Y_draw = yy.reshape(-1,)
X_test = np.c_[X_draw, Y_draw]
predicted_result = logistic_reg_output(X_test).numpy()결정경계를 확인하려고 합니다.
from matplotlib import colors
divnorm=colors.TwoSlopeNorm(vmin=0., vcenter=0.5, vmax=1)
plt.figure(figsize=(10,8))
plt.scatter(X_draw, Y_draw, c=predicted_result, cmap="seismic", norm=divnorm)
plt.colorbar()
plt.scatter(X[:,0], X[:, 1], s=200, c=y, cmap="seismic", norm=divnorm)
plt.show()최종적인 결정경계를 볼 수 있지요.
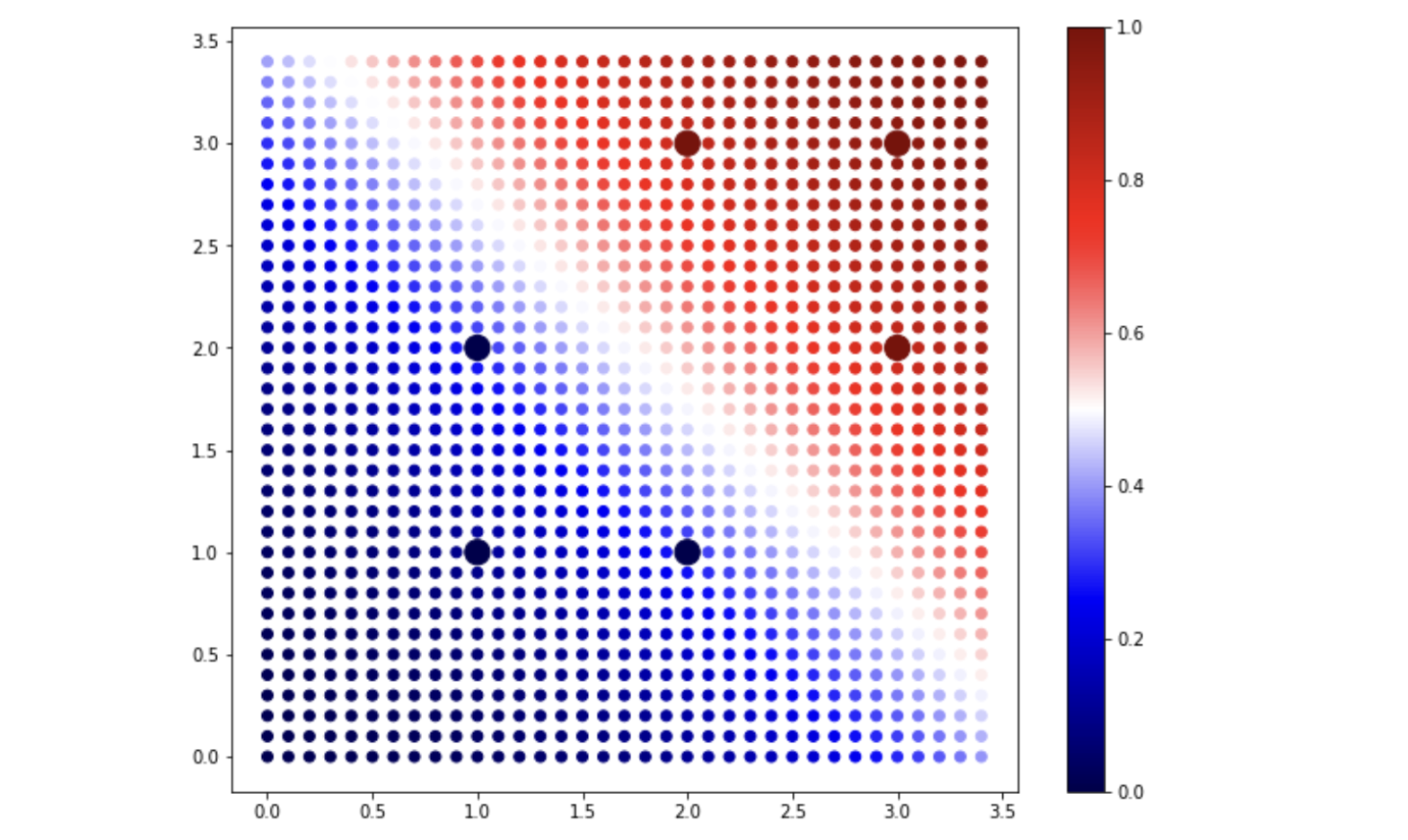
데이터 사이에 잘 만들어진걸로 보이네요.
def logistic_reg_output(X, W, b):
z = tf.matmul(X, W) + b
return 1 / (1 + tf.exp(-z))이번에는 학습 중간 중간의 결정경계의 변화를 보기 위해 logistic_reg_output 함수를 살짝 변경하고~
plt.figure(figsize=(12,10))
idx = 0
for i in [0, 3, 7, 10, 15, 49]:
predicted_result = logistic_reg_output(X_test, hist_W[i], hist_b[i]).numpy()
idx += 1
plt.subplot(2,3,idx)
plt.title(str(i))
plt.scatter(X_draw, Y_draw, c=predicted_result, cmap="seismic", norm=divnorm)
plt.scatter(X[:,0], X[:, 1], s=200, c=y, cmap="seismic", norm=divnorm)
plt.show()이렇게 그리라고 했습니다.^^
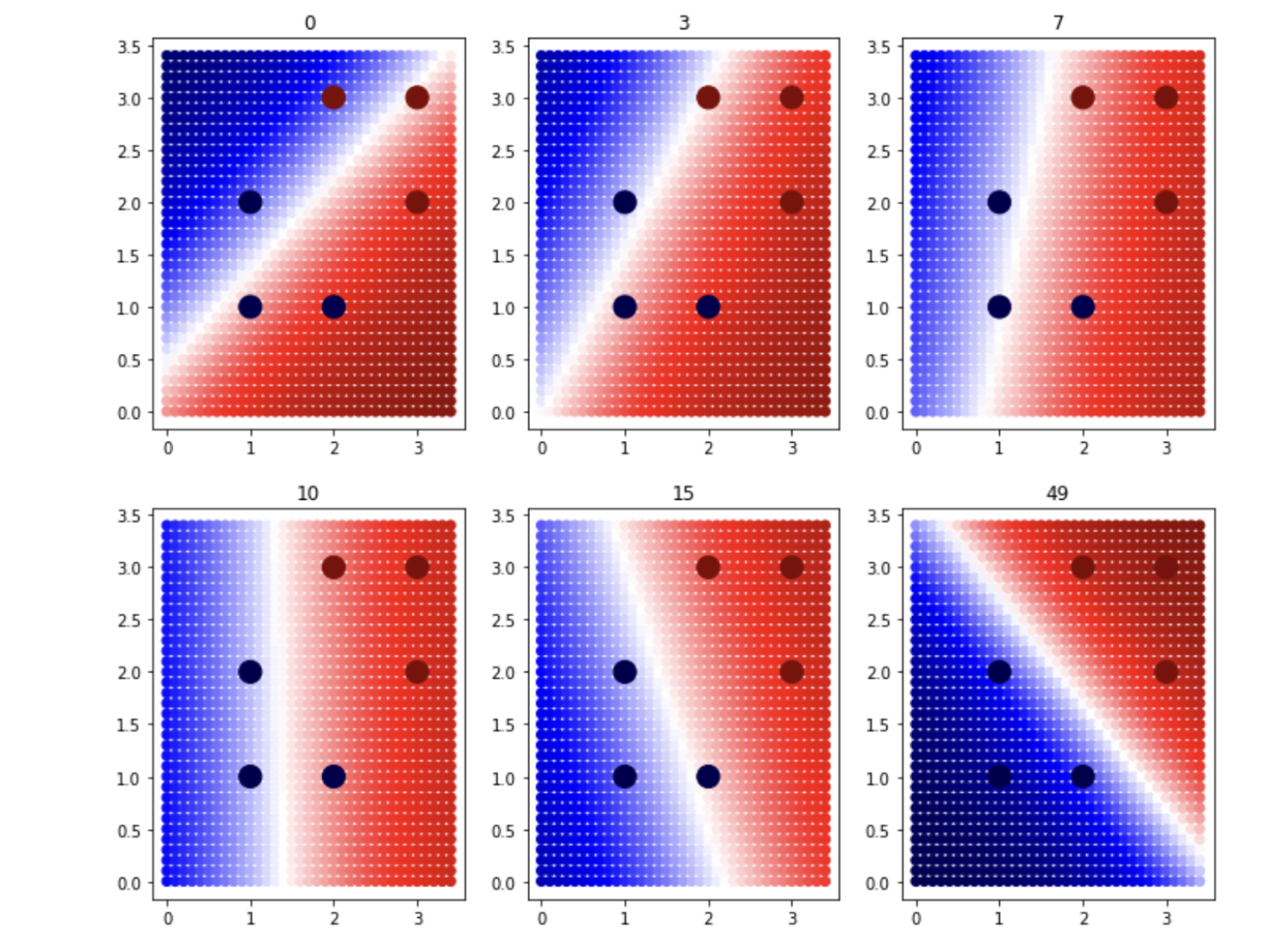
어떤가요 경계면이 변해가는 것이 보이나요~?^^
영상으로 다시 보기
'Theory > DeepLearning' 카테고리의 다른 글
| 영상 인식에 필요한 기초 기법 간편 정리 - ArUCo Marker, YOLO 등 (3) | 2023.06.19 |
|---|---|
| Cost Function 비용함수와 Gradient Descent 경사하강법의 이해 (feat. tensorflow GradientTape) (5) | 2022.03.08 |
| Tensorflow의 GradientTape을 이용한 미분 (2) | 2022.02.18 |
| 어찌어찌 설치하고 구동해본 영상 인식 - CUDA, OpenCV, darknet - YOLO, 그리고 고마운 분들~ (30) | 2018.05.23 |
| [Keras] 붓꽃 Iris 데이터 분류해보기 Iris classification using Keras (30) | 2018.05.18 |
| Python에서 OpenCV를 통해 내가 손으로 쓴 숫자 영역 확인하기 (42) | 2018.05.08 |
| Python에서 OpenCV를 이용해서 초간편하게 사람 얼굴, 몸을 인식하기 (42) | 2018.04.27 |



