아마 딥러닝이 되었든 혹은 간단한 선형 회귀 알고리즘만 공부하려고 해도 비용함수라고 하는 Cost Function(loss funciton)이라고 하는 단어를 만났을 겁니다. 특히 그 후 꼭 따라 붙는 Gradient Descent 경사하강법이라는 단어도 만났을 겁니다. 제가 글을 쓰는 습관이 작은 주제를 나눠서 쓰는 것이라서 비용함수와 경사하강법을 다루어야겠다고 생각했는데, 그것 때문에 참 많은 시간을 들였습니다. 어떤 사람들보다 더 잘 설명해야지 하는 생각은 없었지만, 그래도 이왕 쓰는 것이라 좋은 설명을 해야할텐데... 하는 걱정 때문이었습니다ㅠㅠ. 잘 하고 있는 것인지는 잘 모르겠지만, 그래도 일단 준비한 내용으로 글을 시작해보려고 합니다. 이번 글은 Cost Function이라는 아이를 설명하고 비용함수를 최소로 하는 방법 중 경사하강법이라는 아이를 이야기를 해보려고 합니다.
데이터의 준비
매우 실용적이고 재미있는 데이터를 준비하면 좋겠지만, 이번에는 그렇게 하지 않고 딱 점 세 개... 넵.. 딱 세 개만 가지고 이야기를 하려고 합니다. 이번 글은 Jupyter Notebook에서 실행하고 있으며 파이썬 버전은 3.8입니다. 나머지 모듈들은 대부분 pip 명령으로 버전은 신경쓰지 않고 단순히 설치했습니다.
import numpy as np
import matplotlib.pyplot as plt
x = np.array([2, 3, 5])
y = np.array([1, 5, 6])
plt.scatter(x, y);위 코드의 실행 결과는...
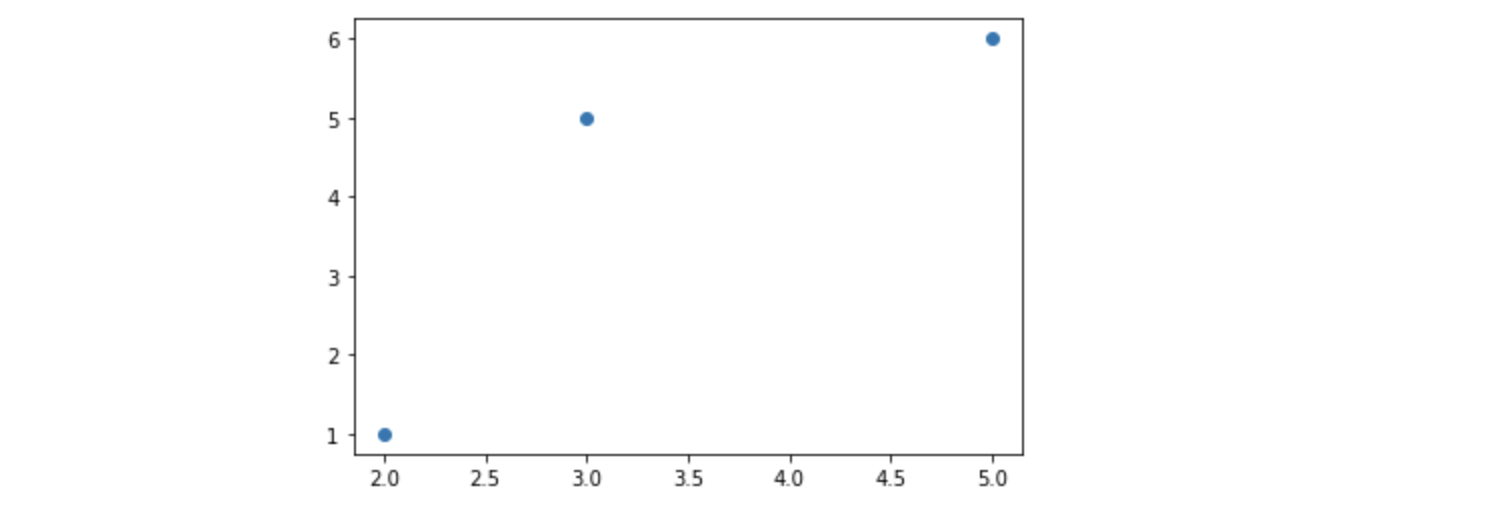
이렇습니다. 그저 x가 2, 3, 5일때 y는 1, 5, 6의 값을 가지도록 한, 딱 점 세 개가 데이터입니다.
얻고 싶은 것~ 데이터를 가장 잘 표현할 수 있는 - 직선
그럼 우리가 얻고 싶은 건 뭘까요. 앞서서 준비한 데이터를 가장 잘 표현할 수 있는 직선입니다.
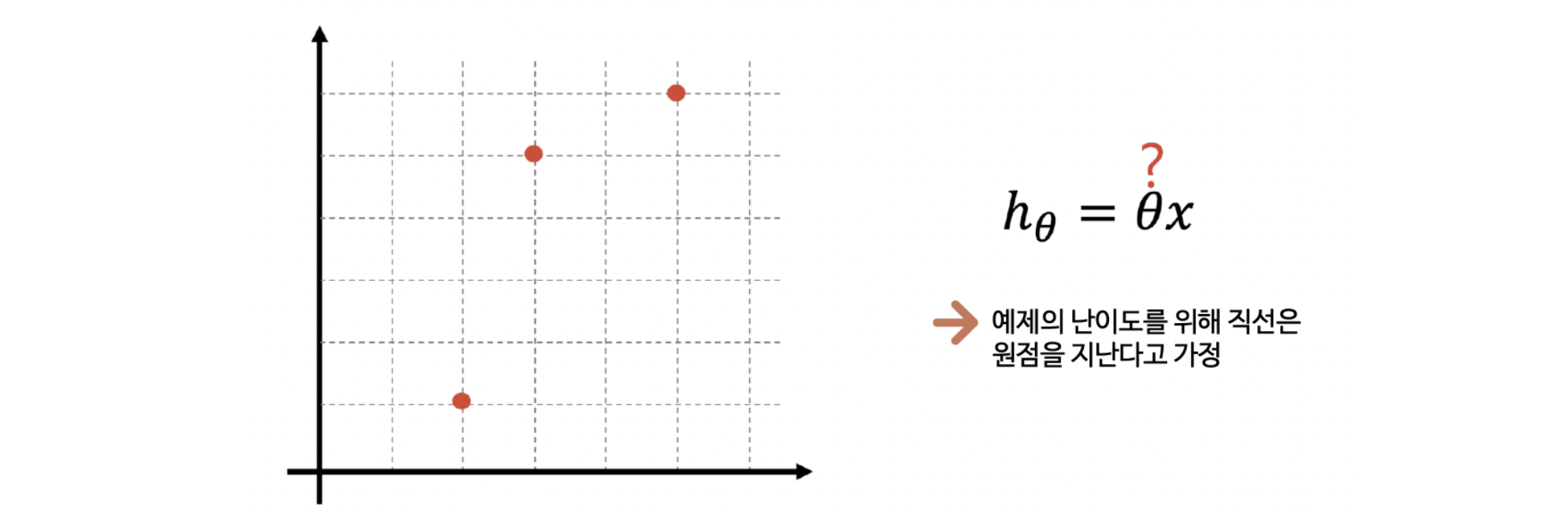
넵. 우리는 직선을 얻고 싶습니다. 먼저 특성(x)과 그에 맞는 답(y)을 주고, 이렇게 데이터는 이산(discrete) 데이터로 간격이 있지만, 얻고 싶은 것은 연속된 값일 때 우리는 회귀문제라고 합니다. 우리는 지도학습 중에서 회귀 문제에 대한 이야기를 하려고 합니다. 원래 직선은 흔히 (중학교 용어로) 기울기와 y 절편이 필요하지만, 손으로도 풀거라 이해를 위해 직선이 원점을 지난다고 생각하겠습니다. 즉 y절편은 0인 것이지요.
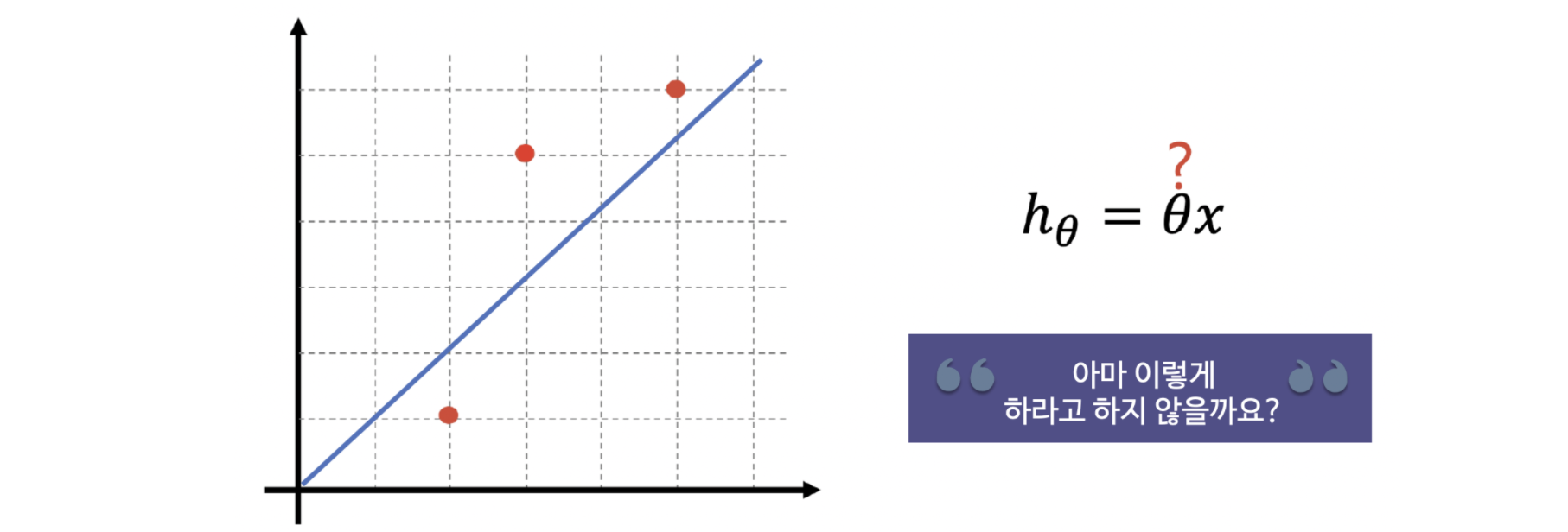
아마 눈으로 대충 점 세 개를 가장 잘 표현하는 직선을 그려보라고 하면 정도의 차이는 있겠지만, 위의 그림처럼 다들 그리겠죠? 그런데 그냥 눈으로 그리면 어떤 직선일 때가 가장 좋은건지를 알 수 없습니다. 그러므로 "가장 좋은", 즉 나의 데이터(지금 우리는 점 세 개지만)를 가장 잘 표현하는 직선을 구하기 위해 어떤 후보 직선을 구했다면, 그 후보 직선에 일종의 "점수"를 줄 필요가 있습니다. 그 점수가 낮을 수록 좋은 거든, 그 반대이든 아무튼 점수로 표현을 해야 좋다, 더 좋다, 나쁘다 등의 말을 할 수 있겠죠.
에러를 정의하자 - 내 데이터를 가장 잘 표현하는 모델을 찾기 위해 해야할 일
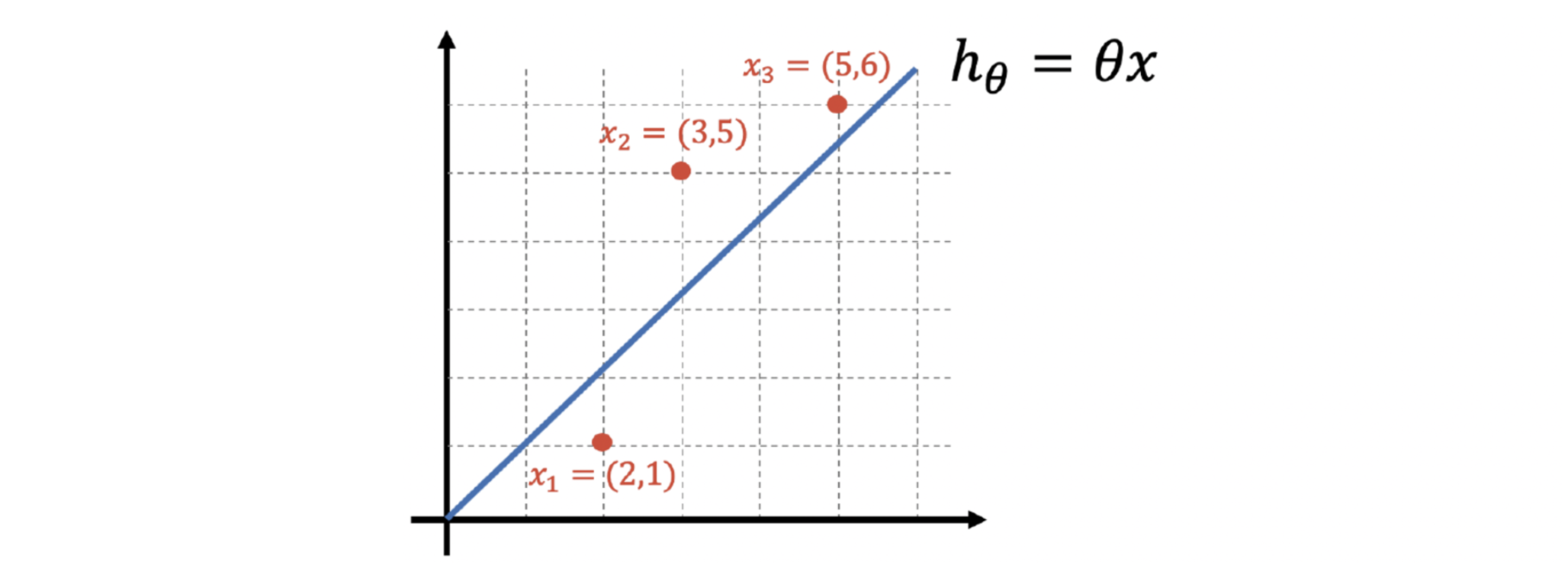
앞서서 우리가 해야할 일은 세 개의 점을 하나의 직선으로 표현하는 것이라고 했습니다. 이제 세 개의 점을 하나의 직선으로 표현하기 위해 직선을 위 그림처럼 생각하기로 했습니다. 이 상태에서 저는 Python의 sympy라는 모듈을 이용해서 잠시 설명을 해 볼까 합니다.

위 그림의 코드처럼 theta를 sympy의 Symbol로 지정하면 문자 연산이 가능해집니다. 나는 원점을 지나는 직선을 가정했으므로 theta*x가 되고, theta를 문자(Symbol)로 지정했으므로 위 글미처럼 각 x 데이터(2, 3, 5)에 대해 각각 theta가 곱해져서 나타나게 됩니다.
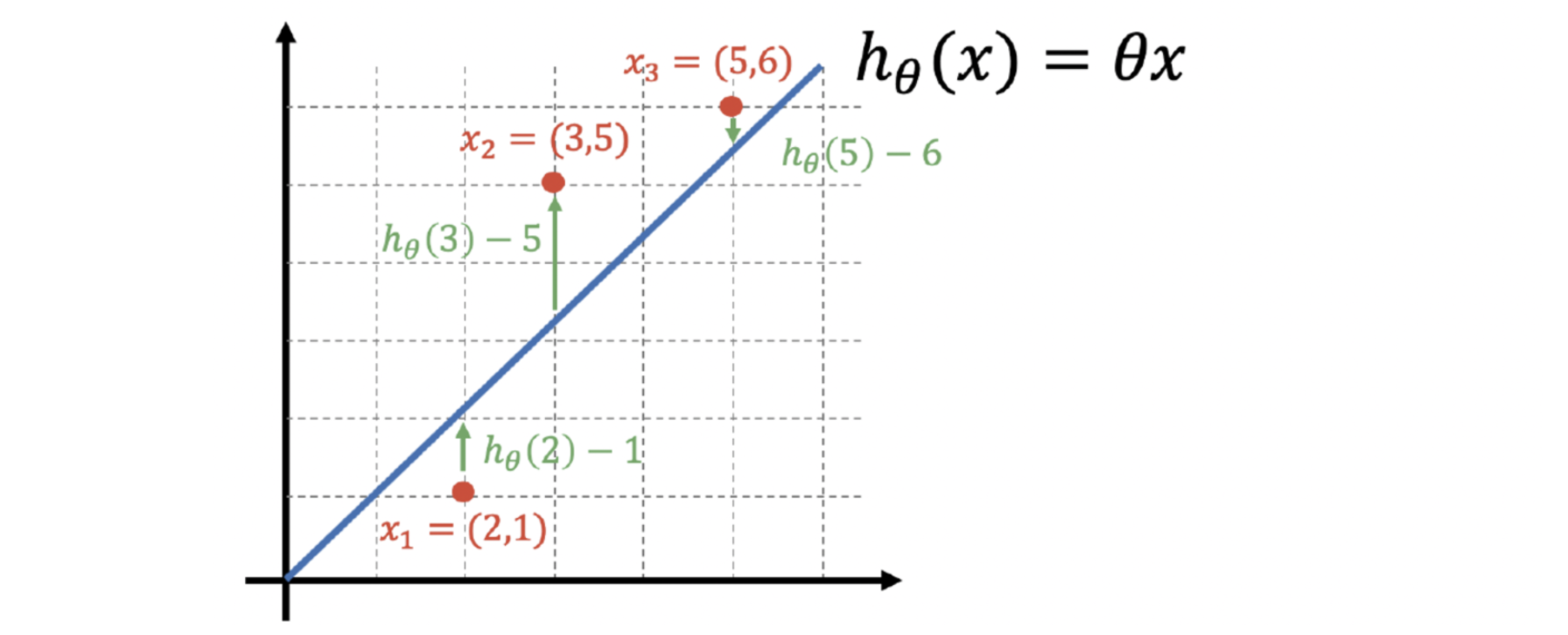
이제 위 그림을 보면, 2theta는 x가 2일때 모델(내가 눈으로 그은^^)의 값이고, 그 때 실제 y값은 1입니다. 그러나 x가 2일때, 예측값(h)과 실제 값의 차이 2theta - 1이 곧 에러(error)가 되는거죠.

그러면 위 그림처럼 각 데이터(실제로는 세 개)의 각 에러는 위 코드처럼 2theta-1, 3theta-5, 5theta-6이 됩니다.
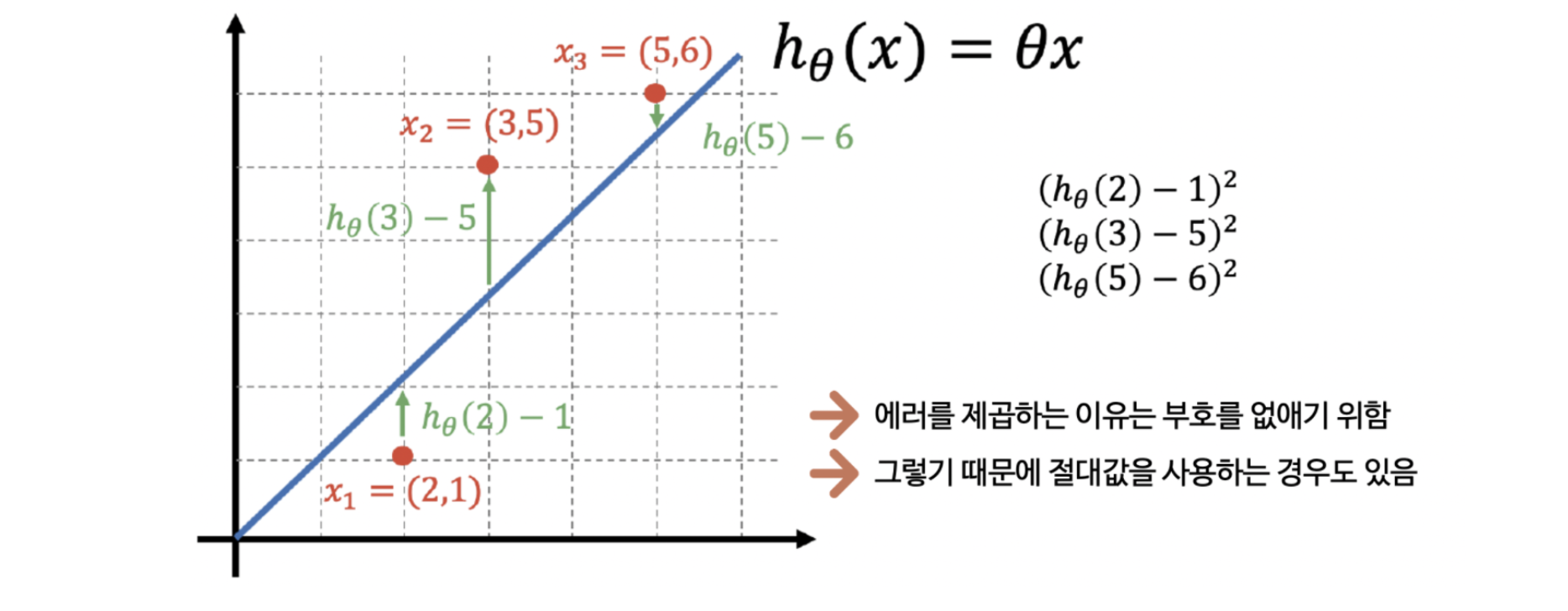
에러의 부호를 일일이 신경쓰는 대신 제곱이라는 간단한 아이를 이용하죠. 방금 코드에서 구한 error라는 변수를 제곱하면 됩니다.

그런데 제곱만 하지 말고, 제곱한 후 평균을 취하면 데이터가 여러개라도 괜찮을 것 같습니다.
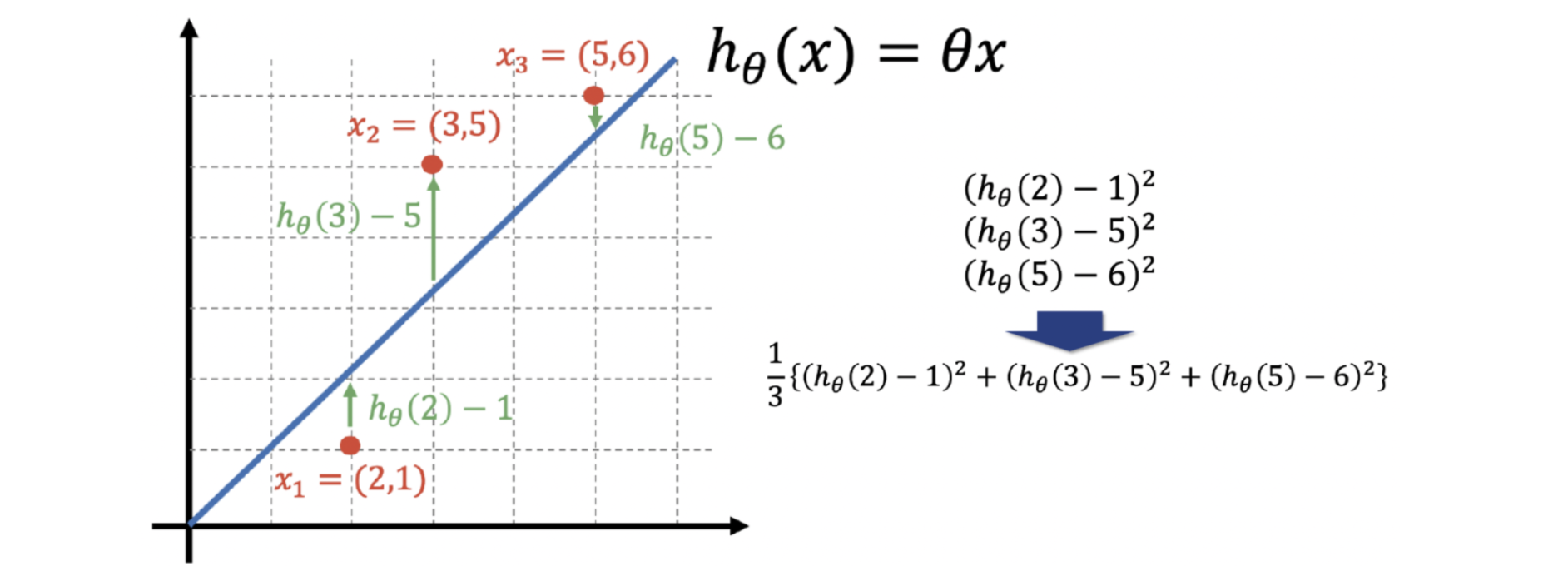
결국 우리가 가정한 직선(데이터 세 개를 잘 표현할 수 있는)을 theta * x라고 했고, 그 모델이 각각의 데이터에 대해 가지는 에러의 제곱의 평균의 식~
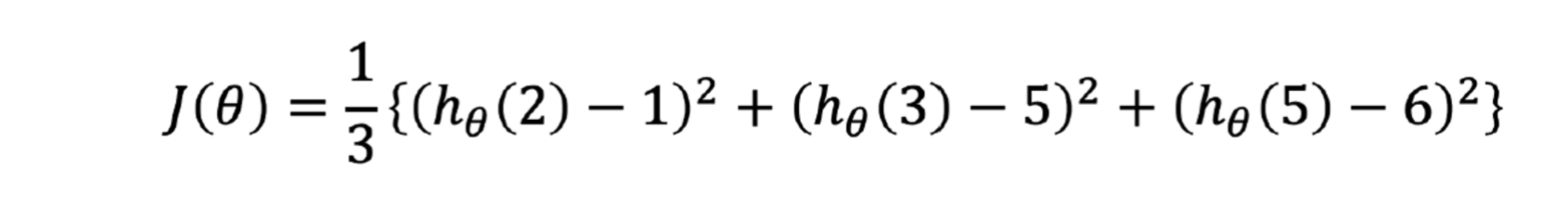
이 식이 Cost Function 비용함수입니다. 항상 에러의 제곱의 평균을 비용함수라고 하는게 아니라 비용함수도 사용자가 여러가지로 정할 수 있습니다. 여기서는 간단해 보이는 저 식을 비용함수라고 하겠습니다. 그럼 다시~ 각 데이터의 모델에 대한 에러로 만든 비용함수 J... 저 비용함수가 최소값을 가진다면 어떨까요. 비용함수가 최소값을 가지면 우리의 모델(직선)이 우리의 데이터를 가장 잘 표현한다고 할 수 있습니다. 이제 우리는 저 비용함수가 최솟값이 되는 theta를 찾는 것이 매우 중요해졌습니다.

Cost Function의 최솟값 찾기 - 미분으로 해볼까?
일단 sympy에서 에러들의 제곱의 평균을 cost라는 이름으로 만들어 두겠습니다.

저 함수는 이차함수입니다. 혹시 어떻게 생겼는지 궁금하시면 sympy의 plotting 모듈의 힘을 조금 빌릴 수 있습니다.
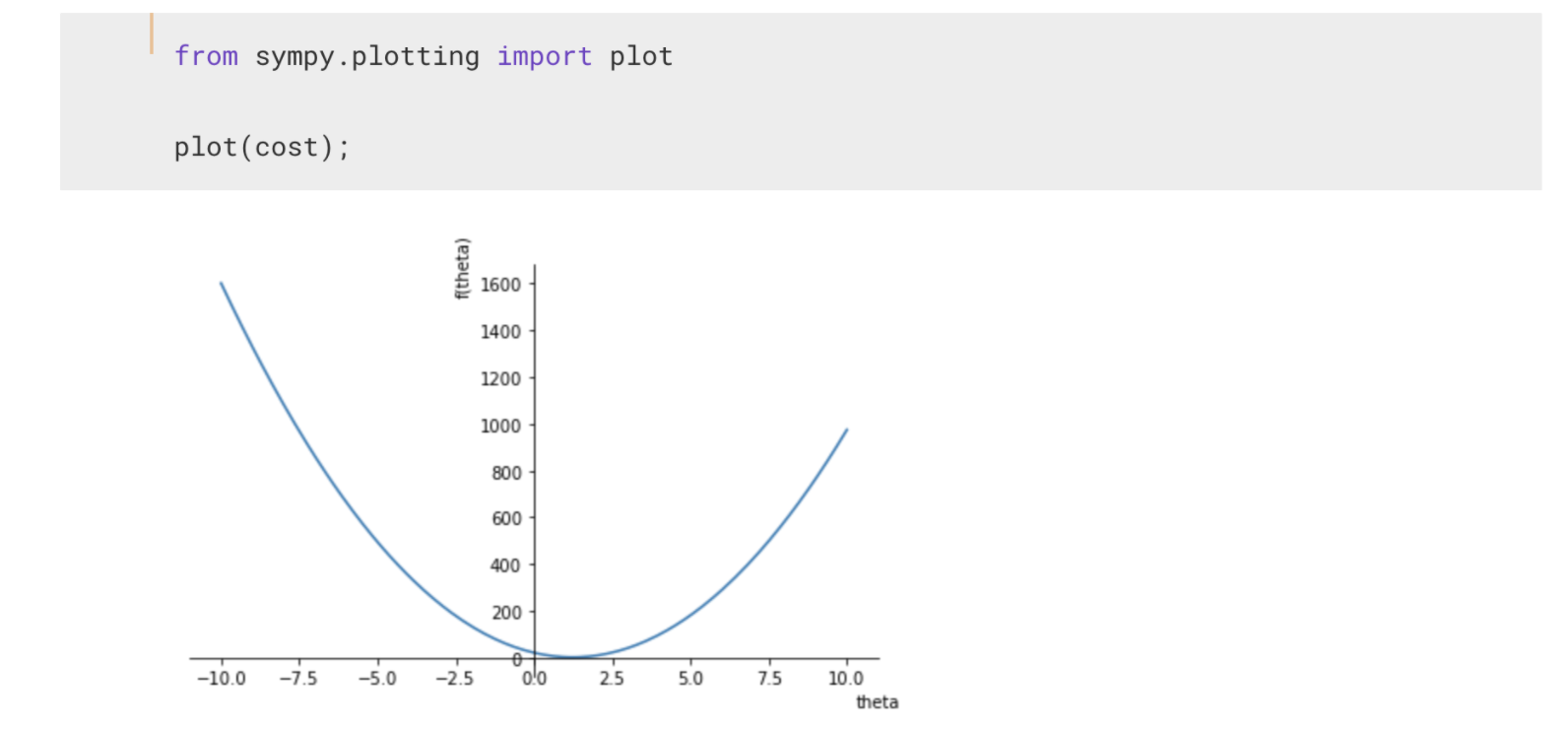
쩌~기, 0과 2.5의 사이쯤이 가장 작은 최솟값이겠네요. 저 그래프의 가장 작은 지점이 되는 theta를 알아 내는 것이 목표입니다. 사실 저 간단한 2차 함수는 미분이 0이 되는 지점, 극값이라고 하는 지점을 구하면 됩니다. cost를 미분해서 0이라고 하고 풀어서 나온 theta가 cost를 가장 작은 값이 되도록 하는 것이죠.

뭐.. 손으로 구할 수도 있고, 저렇게 sympy를 이용해서 코드로 승부를 볼 수도 있겠죠.^^

그리고 나서 저렇게 solve 함수를 이용해서 풀 수 있습니다. 그런데 이렇게 미분으로 간단히 풀 수 있는건 한정적입니다. 비용함수가 아주 복잡하면 안됩니다. 그러나 이번 글에서는 계속 이 데이터와 방금 사용한 cost function을 설명을 위해 가지고 가도록 하겠습니다.
Cost Function의 최솟값을 찾는 과정 이해하기 - Gradient Descent
이야기의 흐름을 또 점검하면...
- 세 개의 좌표로 된 데이터가 있음 (x는 특성, y는 정답)
- 세 개의 데이터를 가장 잘 표현하는 직선을 찾고 싶음
- 그래서 직선을 모델로 가정(theta * x)하고
- 내가 가정한 모델(수식)과 실제 정답(y) 사이의 에러를 구함
- 그 각각의 에러에 대한 제곱의 평균을 수식으로 구함 -> Cost Function
- 잠시 sympy로 미분을 해서 극값을 찾아 해결했지만, 그건 그저 장난삼아 해본 것이고 실제 cost function은 너무 복잡해서 안 통함
이와 같습니다. 이제 경사하강법이라고 하는 Gradient Descent의 원리와 동작 방법을 확인해 보도록 하겠습니다. 다시 원래의 cost function으로 돌아가기 위해서 Symbol로 선언된 함수를 일반적으로 동작하는 수학함수 처럼 만들어야 겠네요. 그때 사용하는 sympy 모듈이 lambdify 입니다.
from sympy.utilities.lambdify import lambdify
cost_f = lambdify(theta, cost)
diff_cost_f = lambdify(theta, diff_cost)이렇게 해두면 cost function은 cost_f에, 미분한 함수는 diff_cost_f에 지정했습니다.
def draw_proc(x_val):
t = np.arange(0, 5, 0.01)
t_diff = np.arange(x_val-0.5, x_val+0.5, 0.01)
plt.figure(figsize=(10,8))
plt.plot(t, cost_f(t))
plt.plot(t_diff, diff_cost_f(x_val)*(t_diff - x_val) + cost_f(x_val))
plt.scatter([x_val], [cost_f(x_val)], s=100, c='red')
plt.grid()그리고 x_val이라는 값을 넣으면 cost_function과 x_val 주변 범위에서 비용함수를 미분한 함수를 그려주는 코드를 위와 같이 먼저 만들어 둡니다.
Cost Function의 최솟값을 찾는 과정 - 1단계 : 랜덤하게 첫 값 설정하기
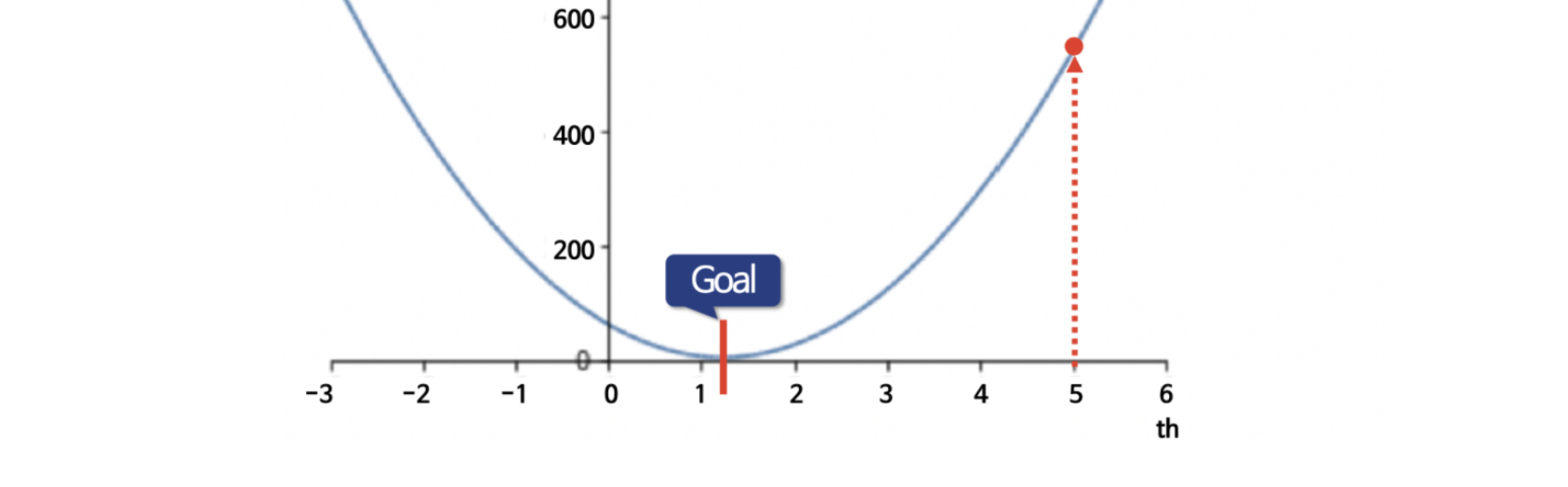
먼저 첫 번째 값을 아무렇게나 랜덤하게 잡습니다.

음.. 위에서는 5라고 했는데 여기서는 4를 잡았네요.ㅠㅠ. 아무튼 랜덤하게 잡았다고 치죠. 그리고 저 4의 위치에서 미분한 값을 계산할 필요가 있습니다.
Cost Function의 최솟값을 찾는 과정 - 2단계 : 비용함수의 미분치를 계산하기
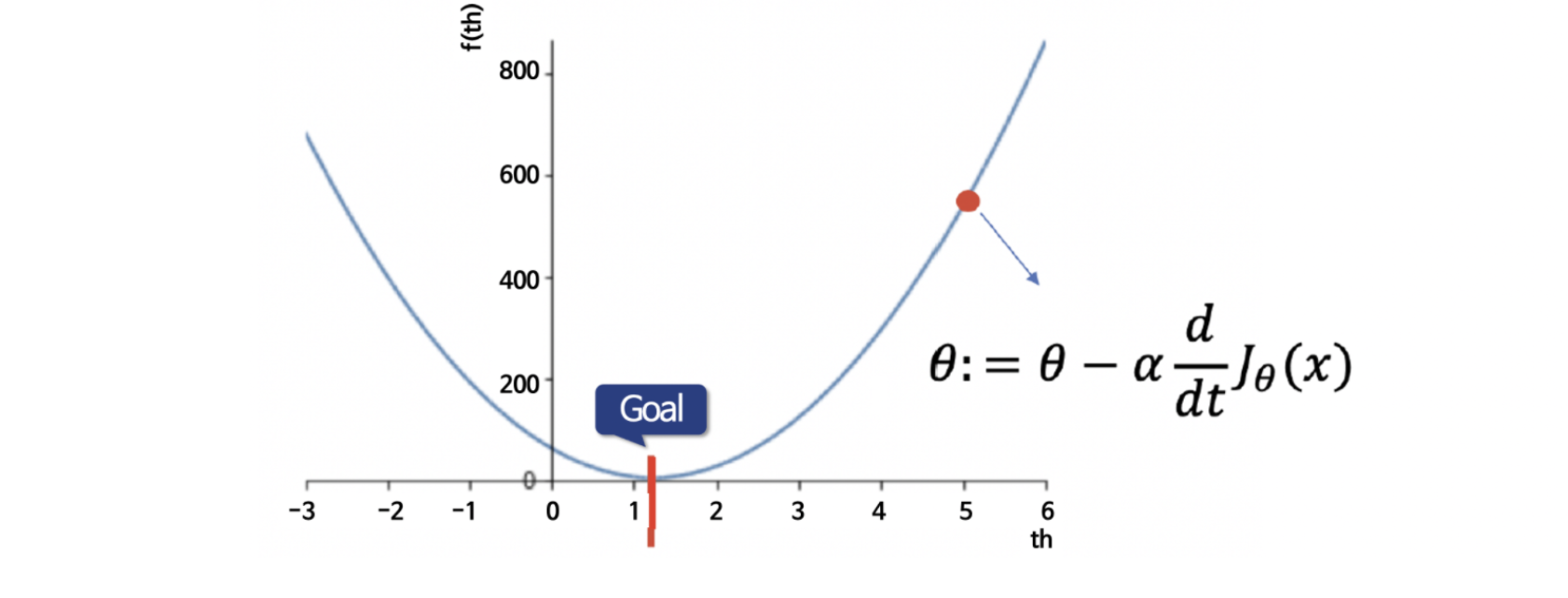
즉, 해당 지점에서 미분을 해보고, 양의 값이 나오면 최솟값(위 그림의 Goal)의 오른쪽에 있는 것이라는 거죠. 미분의 부호가 만약 음수가 나오면 Goal 지점의 왼쪽에 있는 거구요.
def cal_next_step(x_val):
lr = 0.01
current_diff = diff_cost_f(x_val)
current_step = lr*current_diff
print("Current interval : ", current_step)
print("Next X_val : ", x_val - current_step)
return x_val - current_step그래서 위와 같이 함수 하나를 만들어 둡니다. 저 함수는 비용함수를 미분한 함수의 결과에 learning rate을 곱하고 곱한 결과에 현재의 theta를 빼서 새로운 theta를 만들어 내는 것입니다.
Cost Function의 최솟값을 찾는 과정 - 잠시 학습률 learning rate 이해하기

위 식을 보면, 현재의 theta에, 비용함수를 미분하고 learning rate이라는 alpha를 곱하고 빼서, 현재의 theta를 갱신하는 것입니다.
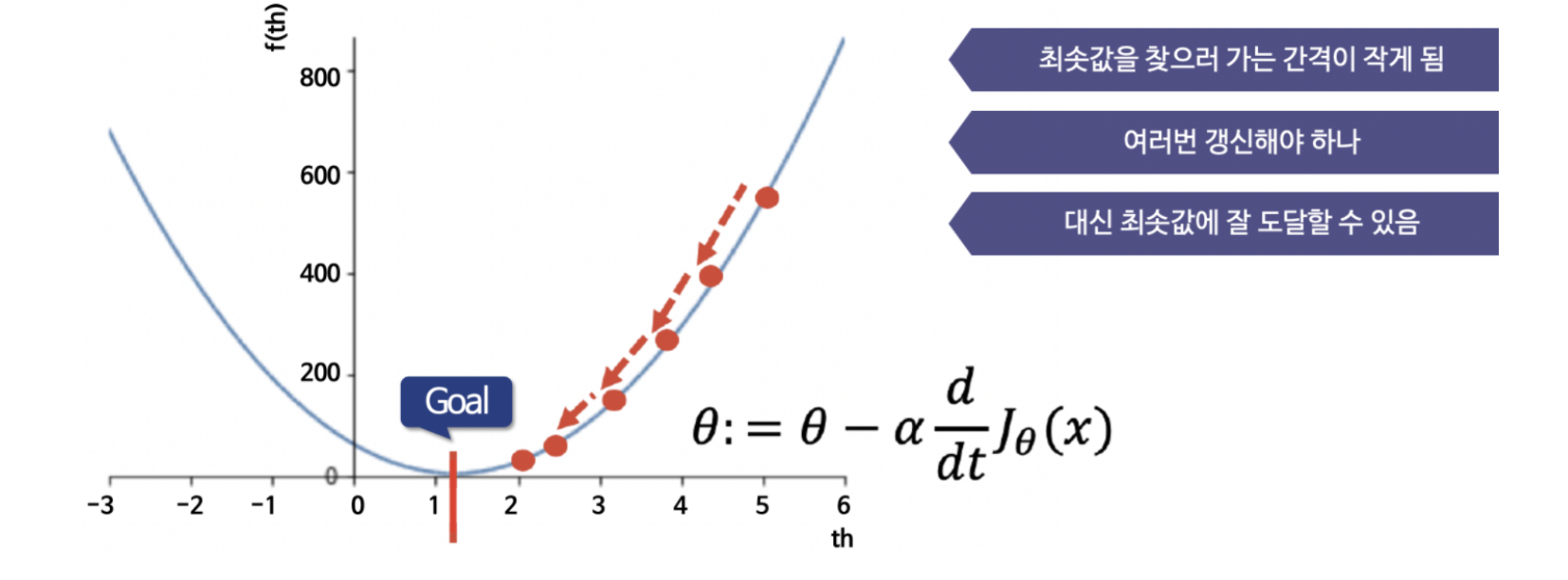
저 학습률(learning rate)이 작은 값이면 Goal을 향해 천천히 다가가게 됩니다.

학습률이 크면 요동을 치면서 내려가거나 혹은 완전히 수렴을 못 할 수도 있습니다.
Cost Function의 최솟값을 찾는 과정 - 3단계 : 미분치를 이용해서 현재 값 갱신하기
일단, 그래서 적장한 학습률을 정했다고 치고, 2단계에서 만든 함수를 이용해서 1단계의 미분치를 계산합니다. 그리고 다음 theta를 찾는거죠.

이제 처음 4였던 theta가 3.3으로 변경되었습니다.
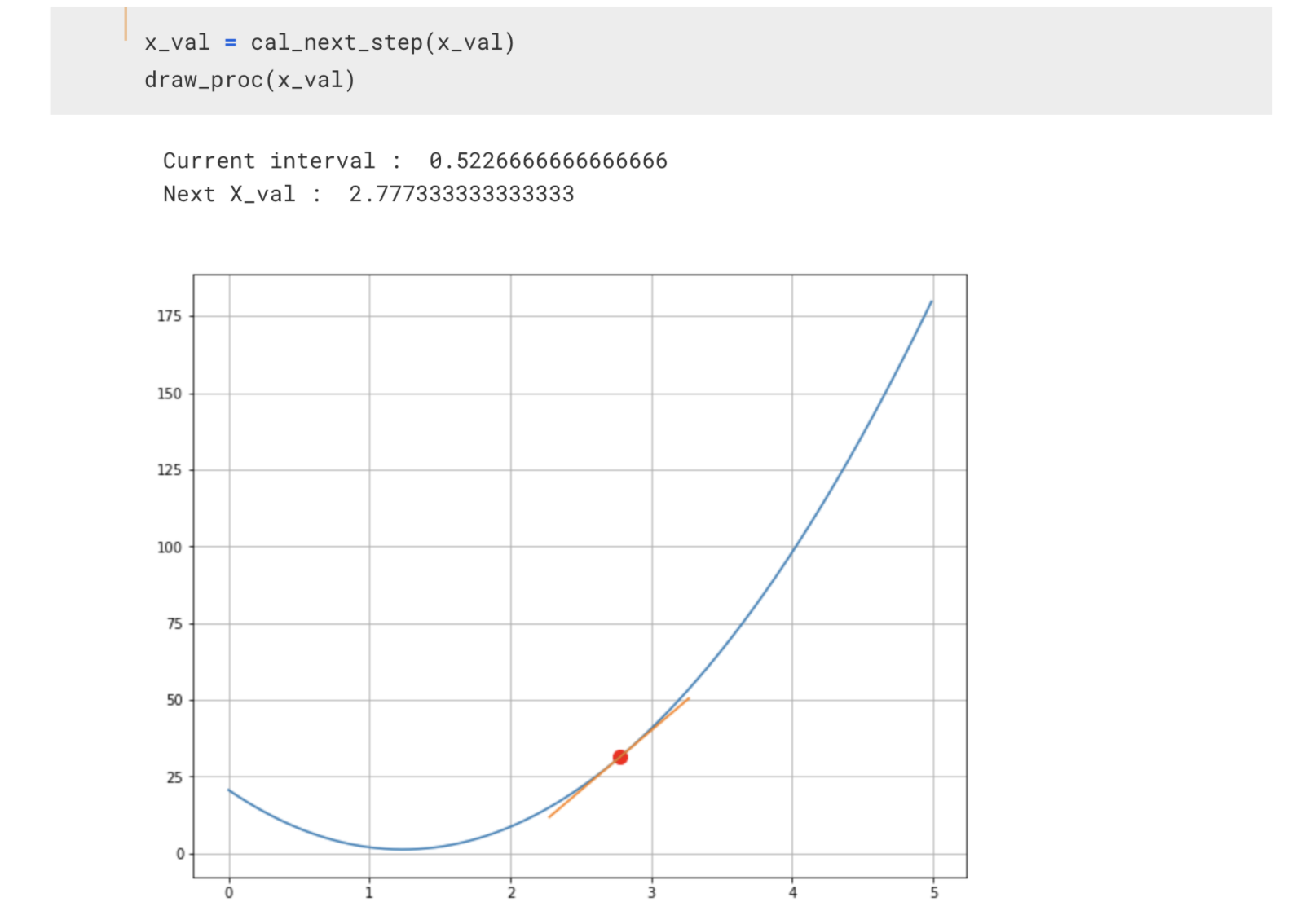
다시 하면 2.77인거죠.
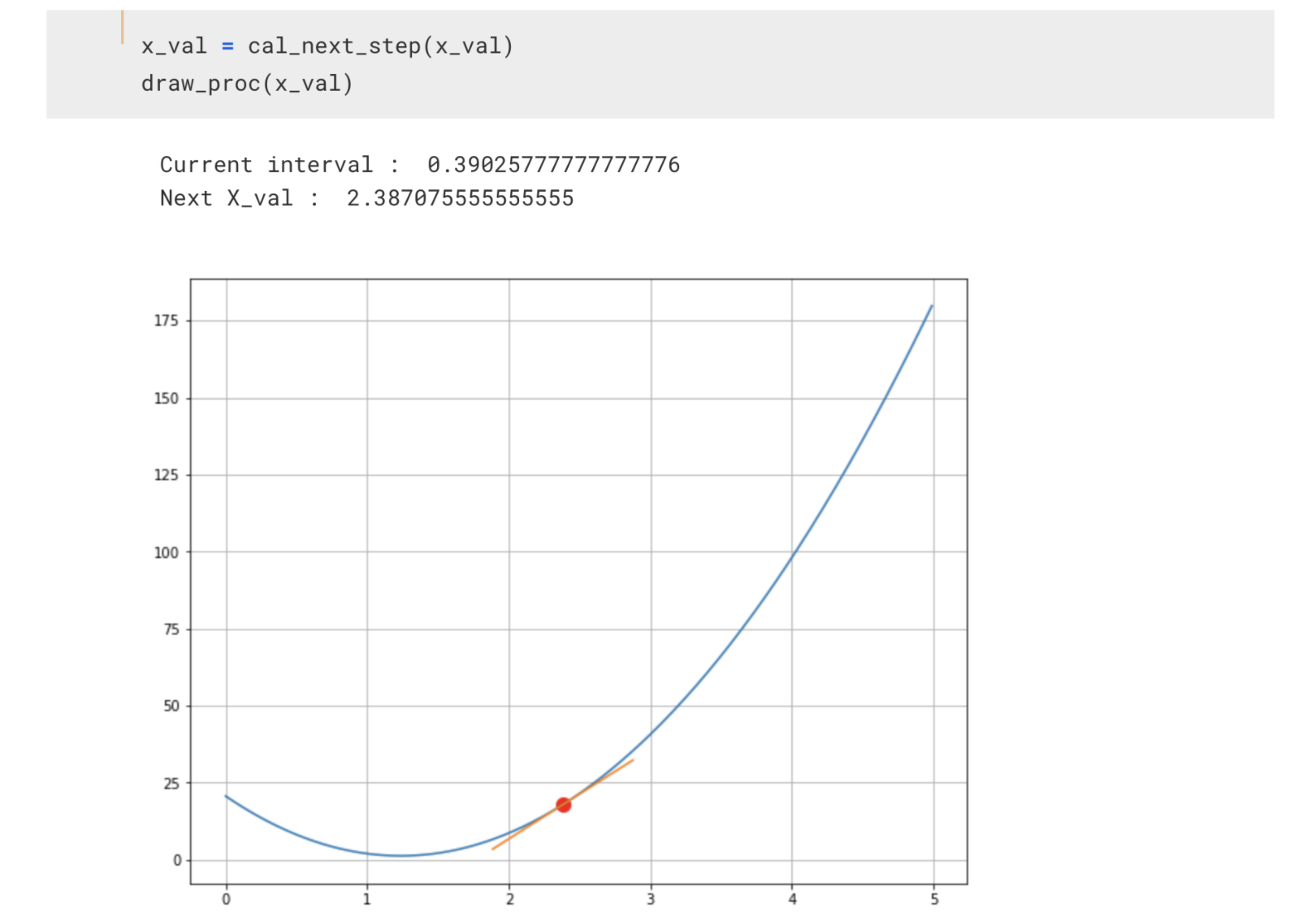
그리고 또 그다음 2.387로 이동하고~ 이렇게 최솟값을 찾아가게 됩니다.
Cost Function의 최솟값을 찾는 과정 - Gradient Descent
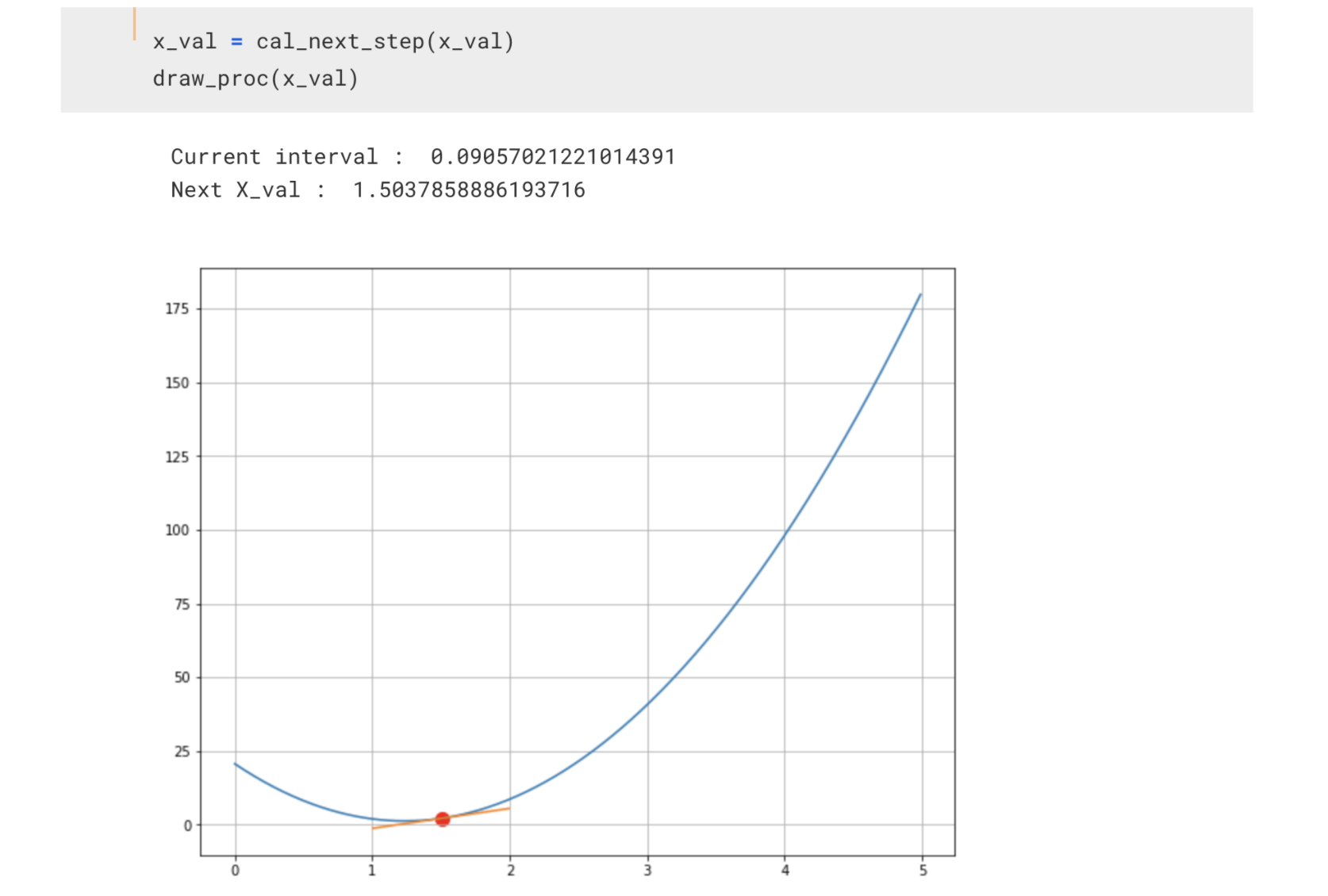
이렇게
- 비용함수를 미분한 함수에 학습률을 곱하고 현재 theta를 갱신하고
- 또 .... 갱신하고~
- 또 .... 갱신하고^^
하는 과정을 계속 반복하는 것이 Gradient Descent, 경사하강법입니다. 여기서 한 가지 주의하실 것은 정확히 들어나지 않아서 찾기 어렵겠지만, 나중에 SGD라는 것을 할 때 기억하셔야할 것인데요. 현재 Gradient Descent를 수행할때는 한 번 theta를 업데이트 할 때마다 계산하는 cost와 미분은 모두 전체 데이터(점 세 개^^)를 모두 사용하고 있습니다.
Gradient Descent - 이제 Tensorflow의 GradietnTape으로 진행해보기
앞서 Cost Function과 Gradient Descent에 대해 이해를 해 보았습니다. 데이터가 복잡하고 그래서 코드도 복잡해지면 일일이 다 내가 코드를 작성하기는 어렵습니다. 그래서 framework을 사용하는거죠. 이번에는 지난번에 살짝 소개를 한 Tensorflow의 GradientTape을 이용해서 진행해 보겠습니다.
Tensorflow의 GradientTape을 이용한 미분
오랜만에 텐서플로우 이야기를 하네요. 뭐 사실 크게 중요하다기 보다는 최근 어떤 자료를 만들다가 이 부분을 추가했는데 그걸 블로그에도 공개하면 좋겠다는 생각이 든것 뿐이랍니다. 오늘은
pinkwink.kr
def linear_reg(x):
return x*W
def mean_squared_error(y_pred, y):
return tf.reduce_sum(tf.pow(y_pred - y, 2)) / (2*n_samples)먼저 선형 모델(linear_reg)를 하나 선언해 두겠습니다. 여기서 W는 앞서서 이야기한 theta와 같다고 생각하시면 됩니다. 딥러닝의 가중치인데 x가 크기가 1이기 때문에 W도 1입니다. 그리고 에러의 제곱의 평균을 계산하는 함수(mean_squared_error)도 미리 작성해 두었습니다.
import tensorflow as tf
lr = 0.001
num_iter = 500
n_samples = x.shape[0]
hist_W = []
W = tf.Variable(np.random.randn())
hist_W.append(W.numpy())
print(W.numpy())그리고 W를 랜덤하게 선언하구요.
for n in range(num_iter):
with tf.GradientTape() as tape:
y_hat = linear_reg(x)
loss = mean_squared_error(y_hat, y)
updated = tape.gradient(loss, W)
W.assign_sub(lr * updated)
hist_W.append(W.numpy())
if n%50==0:
print(n, '\t', ' : Loss : ', loss.numpy(), ' , Weight : ', W.numpy())그리고, num_iter에 지정한 대로 한 500번 반복적으로 W를 갱신하라고 합니다. 이 때 위 코드 내에 gradient를 구하는 부분이 있는 것을 확인할 수 있습니다.

이제 학습이 완료된 W를 이용해서 직선을 만들 수 있는거죠. 저 직선이 아마도 최선이라고 할 수 있을 것 같네요^^
from matplotlib import animation
fig = plt.figure(figsize=(8,6))
ax = plt.axes(xlim=(0, 6), ylim=(0, 7))
dots = ax.scatter(x, y)
line, = ax.plot([], [], lw=2, ls='dashed', color='red')
def init():
line.set_data([], [])
return line,
def animate(i):
t = np.arange(0, 6, 0.01)
line.set_data(t, t*hist_W[i])
return line,
anim = animation.FuncAnimation(fig, animate, init_func=init,
frames=200, interval=20, blit=True)
anim.save('exAnimation.gif', writer='pillow', fps=30, dpi=100)
plt.show()위 코드를 실행하면 매번 갱신되는 W를 hist_W에 저장해 두었는데 그걸 이용해서 직선이 어떻게 변해가는지 알 수 있습니다.

위 빨간 점선의 직선을 보면 Gradient Descent를 이용해서 직선을 찾는 과정을 확인할 수 있을 겁니다.
'Theory > DeepLearning' 카테고리의 다른 글
| 영상 인식에 필요한 기초 기법 간편 정리 - ArUCo Marker, YOLO 등 (3) | 2023.06.19 |
|---|---|
| Tensorflow로 직접 구현하면서 이해하는 Logistic Regression (2) | 2022.04.27 |
| Tensorflow의 GradientTape을 이용한 미분 (2) | 2022.02.18 |
| 어찌어찌 설치하고 구동해본 영상 인식 - CUDA, OpenCV, darknet - YOLO, 그리고 고마운 분들~ (30) | 2018.05.23 |
| [Keras] 붓꽃 Iris 데이터 분류해보기 Iris classification using Keras (30) | 2018.05.18 |
| Python에서 OpenCV를 통해 내가 손으로 쓴 숫자 영역 확인하기 (42) | 2018.05.08 |
| Python에서 OpenCV를 이용해서 초간편하게 사람 얼굴, 몸을 인식하기 (42) | 2018.04.27 |



