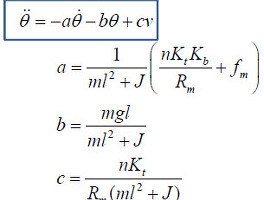이번에는 지난번 선형동역학의 상태방정식 표현에 이어 대표적인 선형제어기인 LQR에 대해 이야기를 할려고합니다. 깊이있는 이야기가 아니라 그저 소개와 함께 실제로는 어떻게 LQR 제어 게인을 얻는지에 관한 이야기입니다.
- Simulation
- 1. 라그랑지 방법을 이용한 동역학 모델 구축하기
- Simulation
- 2. DC 모터의 동역학 포함시키기
- Simulation
- 3. MATLAB을 이용하여 시뮬레이션 구축하기
- Simulation
- 4. 시스템의 선형화
- Simulation
- 5. LQR 기법을 이요한 선형제어기 설계하기
- Simulation
- 6. 경로추적
기본적인 LQR의 개념 !
일반적인 선형시스템의 상태방정식은 dot_X = A*X+B*U의 형태입니다. 거기서 제어입력 U를
U=-KX
로 두고 다시 정리하면
dot_X=(A-B*K)*X
가 되는데요. 이걸 다시 H=A-BK로 두고 위와 같이 정리해둘 수 있습니다.
일단 성능지표(performance index)라고 하는 것을 위와 같이 생각해 볼 수 있습니다. 위의 상태 X는 벡터의 형태이기 때문에 사실상은 각 상태의 제곱의 합으로 표현한 것입니다. 상태의 제곱의 합이 작을 수록 좋은 것이지요. 결국 위의 정능지표를 최소화하는 뭔가가 필요한 것입니다.
이제 다시 일반적인 시스템에서 위의 수식을 만족하면 시스템은 안정(stable)하다고 볼 수 있습니다. 그러면, 그렇게 만들어주는 행렬 P를 찾으면 되는 것이지요.
그것을 대입해서 정리하면 됩니다. 그러면 위의 마지막 수식에서
이걸 만족하는 P,H를 찾으면 되죠. 문제는 식하나에 미지수가 2개네요.
처음 생각했던 성능지표에 다시 대입해서 풀면
를 찾을 수 있습니다. 이제
위의 1,2번 식을 만족하는 미지수 P,H를 찾으면, 제어게인 K를 찾을 수 있습니다. 그런데 일반적으로 성능지표는 각 상태에 가중치를 줄 수 있고, 제어입력의 크기에 대해서도 가중치를 설정할 수 있도록
를 많이 사용하는 편입니다. 문제는 성능지표를 저렇게 두면, 손으로 푸는게 좀 어렵고 귀찮습니다. 그래서 많이 사용하는 것이 당연히 MATLAB이지요^^
MATLAB을 이용한 LQR 게인 구하기 !
지난 시간까지 우리가 다루던 시스템의 상태방정식입니다. 여기서 A, B행렬을 얻을 수 있지요.
그리고, Q, R을 적절히 선정하고 MATLAB에서 LQR이라는 명령을 사용해주면 끝납니다.^^ 쉽죠^^
위 그림은 시뮬링크에서 LQR게인을 적용한 부분입니다.
이것은 그 결과이지요. 자유운동을 시켰을 때 보다 확실히 성능이 좋아졌네요. 이렇게 되면, 아마 Q, R값을 조절해 보면 좀더 성능이 좋아 질 것입니다.^^
'Theory > Lecture' 카테고리의 다른 글
| [엑셀 연재] 2. 자동 채우기와 데이터 유효성 (2) | 2010.09.13 |
|---|---|
| [엑셀 연재] 1. 주간계획표를 만들어보자... (20) | 2010.08.30 |
| [시스템 시뮬레이션 연재] 6. 경로추적 (tracking) (29) | 2010.08.16 |
| [시스템 시뮬레이션 연재] 4. 시스템의 선형화 (3) | 2010.08.12 |
| [시스템 시뮬레이션 연재] 3. 동역학 MATLAB으로 시뮬레이션 하기 (20) | 2010.08.11 |
| [시스템 시뮬레이션 연재] 2. 구동원으로 DC 모터 고려하기 (64) | 2010.08.11 |
| [시스템 시뮬레이션 연재] 1. 라그랑지 방법을 이용한 동역학 모델 구축하기 (28) | 2010.08.09 |