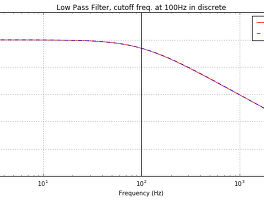
얼마전에 보드선도를 그리는 것에 대한 기초를 이야기[바로바기] 했었는데요. 그 때 그 글에서 보여주었던 예쁘장한(^^) 그래프는 Python에서 그렸었습니다. 오늘은 Bode 선도를 Python에서 어떻게 그리는가와 그 때 그 글에서처럼 그래프로 표현을 어떻게 하는가를 이야기할까 합니다.^^
import numpy as np from scipy import signal import matplotlib.pyplot as plt
일단 수치연산에서는 뭐 필수라고 하는 numpy와 그래프 표현에 필요한 matplotlib를 import하구요. 추가로 scipy의 signal을 import 하도록 하겠습니다. 그리고, 나서
s1 = signal.lti([1], [1, 1]) w, mag, phase = signal.bode(s1, np.arange(0.01, 100.0, 0.01).tolist())
signal의 lti를 이용해서
를 표현합니다. 아... a=1이라고 생각했습니다.^^ 그리고 나서 signal의 bode 명령으로 원하는 주파수 범위와 주파수 간격을 정해주면 주파수축(w)과 크기(mag), 위상(phase)을 얻을 수 있습니다.^^. 남은건 그저 저 아이를 그리는 것 뿐입니다. 너무 간단하죠^^
plt.figure(figsize=(15,8)) plt.subplot(2,1,1) plt.semilogx(w, mag, lw=5) # Bode magnitude plot plt.ylim([-40, 1]) plt.xlabel('Hz') plt.ylabel('Magnitude (dB)') plt.grid(True) plt.subplot(2,1,2) plt.semilogx(w, phase, lw=5, label="real bode plot") # Bode phase plot plt.xlabel('Hz') plt.ylim([-91, 1]) plt.ylabel('Phase (deg)') plt.grid(True) plt.show()
한 그림에 크기위 위상을 표현하는 것이고, 보기 좋은 범위로 좀 잘랐습니다. 아~ x축이 로그스케일(log scale)이어서 semilogx라는 명령으로 plot을 했습니다. 그 결과는
와 같습니다^^. 딱~ 봐도 이제는 [바로가기]에서 설명했으니~ 아시겠죠. 그런데 가끔은 이런 지식의 습득도 코드로 확인해보면 정확하게 이해될때가 있습니다.
plt.figure(figsize=(15,5)) plt.semilogx(w, mag, lw=5) # Bode magnitude plot plt.plot([0.01, 1, 100], [0, 0, -40], 'r--', lw=5) plt.annotate('Break Point ($ \omega = a $)', xy=(1,0), xytext=(4,-3), size=15, arrowprops=dict(facecolor='black', shrink=0.04)) plt.plot(1, 0, 'k', linestyle=' ', marker='o', markersize=10) plt.annotate('-20dB/decade', xy=(5,-15), xytext=(1,-25), size=15, arrowprops=dict(facecolor='black', shrink=0.04)) plt.annotate('Actual curve is -3dB below breakpoint', xy=(w[99],mag[99]), xytext=(0.1,-15), size=15, arrowprops=dict(facecolor='black', shrink=0.04)) plt.plot(w[99], mag[99], 'k', linestyle=' ', marker='o', markersize=10) plt.text(0.05, -30, r"$ H(S)= \frac{a}{s+a} $", size=30, horizontalalignment='center', verticalalignment='center') plt.ylim([-40, 1]) plt.ylabel('Magnitude (dB)') plt.grid(True) plt.figure(figsize=(15,5)) plt.semilogx(w, phase, lw=5, label="real bode plot") # Bode phase plot plt.plot([0.01, 1/5, 5, 100], [0, 0, -90, -90], 'r--', lw=5, label="aymptote line") plt.axvline(1/5, color='k', lw=2, ls='dashed') plt.axvline(5*1, color='k', lw=2, ls='dashed') plt.annotate('$ \omega = a/5 $', xy=(1/5, -90), xytext=(0.1,-80), size=15, arrowprops=dict(facecolor='black', shrink=0.04)) plt.annotate('$ \omega = 5a $', xy=(5*1, -90), xytext=(10,-80), size=15, arrowprops=dict(facecolor='black', shrink=0.04)) plt.annotate('Break Point ($ \omega = a $)', xy=(1,-45), xytext=(3,-15), size=15, arrowprops=dict(facecolor='black', shrink=0.04)) plt.plot(1, -45, 'k', linestyle=' ', marker='o', markersize=10) plt.text(0.05, -60, r"$ H(S)= \frac{a}{s+a} $", size=30, horizontalalignment='center', verticalalignment='center') plt.ylim([-91, 1]) plt.ylabel('Phase (deg)') plt.legend() plt.grid(True) plt.show()
예를 들면 위 코드처럼 말이죠. 학습하는 공식을 이용해서 방금 그래프 위에 주석들을 달아보는거죠^^ 뭐.. 물론 잉여스러운 일이긴 합니다만^^
그렇게 해서 얻은 그래프 중 크기(mag) 부분이네요^^
이번에는 2차계를 표현해볼까요^^
zeta = np.array([0.05, 0.15, 0.5]) s1 = signal.lti([1], [1, 2*zeta[0], 1]) s2 = signal.lti([1], [1, 2*zeta[1], 1]) s3 = signal.lti([1], [1, 2*zeta[2], 1]) w, mag1, phase1 = signal.bode(s1, np.arange(0.01, 100.0, 0.01).tolist()) w, mag2, phase2 = signal.bode(s2, np.arange(0.01, 100.0, 0.01).tolist()) w, mag3, phase3 = signal.bode(s3, np.arange(0.01, 100.0, 0.01).tolist())
2차계는 zeta의 값에 따른 변화가 있으므로 대표적으로 3개 정도 값으로 해서 구하도록 하겠습니다.
plt.figure(figsize=(15,8)) plt.subplot(2,1,1) plt.semilogx(w, mag1, lw=5, color="blue", label="$ \zeta = 0.05 $") # Bode magnitude plot plt.semilogx(w, mag2, lw=5, color="green", label="$ \zeta = 0.15 $") plt.semilogx(w, mag3, lw=5, color="cyan", label="$ \zeta = 0.5 $") plt.legend() plt.xlabel('Hz') plt.ylim([-81, 30]) plt.ylabel('Magnitude (dB)') plt.grid(True) plt.subplot(2,1,2) plt.semilogx(w, phase1, lw=5, color="blue", label="$ \zeta = 0.05 $") # Bode phase plot plt.semilogx(w, phase2, lw=5, color="green", label="$ \zeta = 0.15 $") plt.semilogx(w, phase3, lw=5, color="cyan", label="$ \zeta = 0.5 $") plt.legend() plt.grid(True) plt.ylim([-185, 5]) plt.xlabel('Hz') plt.ylabel('Phase (deg)') plt.show()
위 코드로 plot을 해보면
이렇게 이쁘게 얻을 수 있습니다. Python에서는 plot 명령에 옵션으로 label을 지정하면 손 쉽게 legend를 표현할 수 있습니다. 여기서 좀 더 양념을 치면~
import matplotlib.patches as patches zeta = np.array([0.05, 0.15, 0.5]) s1 = signal.lti([1], [1, 2*zeta[0], 1]) s2 = signal.lti([1], [1, 2*zeta[1], 1]) s3 = signal.lti([1], [1, 2*zeta[2], 1]) w, mag1, phase1 = signal.bode(s1, np.arange(0.01, 100.0, 0.01).tolist()) w, mag2, phase2 = signal.bode(s2, np.arange(0.01, 100.0, 0.01).tolist()) w, mag3, phase3 = signal.bode(s3, np.arange(0.01, 100.0, 0.01).tolist()) plt.figure(figsize=(15,5)) plt.semilogx(w, mag1, lw=5, color="blue", label="$ \zeta = 0.05 $") # Bode magnitude plot plt.semilogx(w, mag2, lw=5, color="green", label="$ \zeta = 0.15 $") plt.semilogx(w, mag3, lw=5, color="cyan", label="$ \zeta = 0.5 $") plt.plot([0.01, 1, 100], [0, 0, -80], 'r--', lw=5) plt.annotate('Break Point ($ \omega = \omega_{n} $)', xy=(1,0), xytext=(0.05,-20), size=15, arrowprops=dict(facecolor='black', shrink=0.04)) plt.axvline(1, color='k', lw=3, ls='dashed') plt.plot(1, 0, 'k', linestyle=' ', marker='o', markersize=10) plt.annotate('-40dB/decade', xy=(5,-25), xytext=(10,-15), size=15, arrowprops=dict(facecolor='black', shrink=0.04)) currentAxis = plt.gca() currentAxis.add_patch( patches.Rectangle( (0.5,-75), 1.5, 100, fill=False, edgecolor='black', linewidth=3, linestyle='dotted', zorder = 10 ) ) plt.annotate('Resonant Peak : $ 1/(2 \zeta ) $', xy=(2,20), xytext=(4,20), size=15, arrowprops=dict(facecolor='black', shrink=0.04)) plt.text(10,10, 'Actual Max. : $ 1/ ( 2 \zeta \sqrt{ 1-\zeta^2 } ) $', size=15, horizontalalignment='center', verticalalignment='center') plt.text(0.05, -60, r"$ H(S)= \frac{\omega_n^2 }{(s^2 +2\zeta\omega_n s + \omega_n^2)} $", size=30, horizontalalignment='center', verticalalignment='center') plt.ylim([-81, 30]) plt.ylabel('Magnitude (dB)') plt.legend() plt.grid(True) plt.figure(figsize=(15,5)) plt.semilogx(w, phase1, lw=5, color="blue", label="$ \zeta = 0.05 $") # Bode phase plot plt.semilogx(w, phase2, lw=5, color="green", label="$ \zeta = 0.15 $") plt.semilogx(w, phase3, lw=5, color="cyan", label="$ \zeta = 0.5 $") plt.annotate('Break Point ($ \omega = \omega_{n} $)', xy=(1,-90), xytext=(3,-30), size=15, arrowprops=dict(facecolor='black', shrink=0.04)) plt.plot(1, -90, 'k', linestyle=' ', marker='o', markersize=10) plt.text(0.05, -120, r"$ H(S)= \frac{\omega_n^2 }{(s^2 +2\zeta\omega_n s + \omega_n^2)} $", size=30, horizontalalignment='center', verticalalignment='center') plt.legend() plt.grid(True) plt.ylim([-185, 5]) plt.ylabel('Phase (deg)') plt.show()
위 코드의 결과는
크기와
위상을 이렇게 그리도록 한 것입니다. 특히 화면상에 box를 matplotlib의 patches을 이용했습니다.~ 뭐 그냥 메인 그림만 그려서 power point같은 곳에서 해도 되지만, 추후 수정하는 것을 생각하면 요런 스타일도 괜찮지 않을까 해요^^
'Software > Python' 카테고리의 다른 글
| Python으로 구현해보는 Band Pass Filter (18) | 2016.09.08 |
|---|---|
| Python으로 구현해보는 1차 고역통과필터 (8) | 2016.09.01 |
| Python으로 구현해 보는 디지털 저역통과필터 (1차 Low Pass Filter) (30) | 2016.08.26 |
| IPython Notebook에서 Markdown 사용하기... (6) | 2016.08.19 |
| Anaconda를 이용한 Python 설치와 Spyder의 편리함 (12) | 2016.08.05 |
| Python에서 그래프를 애니메이션으로 표현하고 GIF로 저장하기 (18) | 2016.04.01 |
| 폼 나게 이쁜 그래프 그려보기 - Matplotlib 예제 (24) | 2016.02.10 |