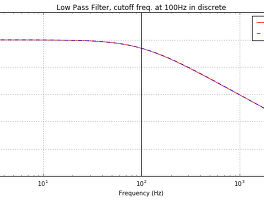
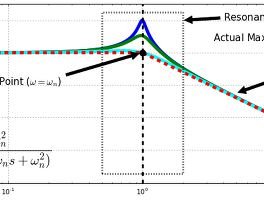
Python에서 구현해 보는 1차 저역통과필터[바로가기]를 이야기했었는데요. 제가 블로그에서 저역통과필터는 많이 이야기했지만, 고역통과필터는 그에 반해 별이야기를 안했더군요. 사실 일반적으로는 신호의 노이즈 등을 제거하는 용도로 저역통과필터를 많이 사용하기 때문에 상대적으로 고역통과필터는 좀 들 다뤄지긴 한듯 합니다. 그래서 이번에는 1차 고역통과필터를 Python에서 구현하는 방법에 대해 이야기를 하겠습니다. 그런데 많은 내용이 지난번 글[바로가기]과 꽤 겹칩니다.^^
연속시간 영역에서의 1차 고역통과필터
사실 저역과 고역통과필터는 꽤 닮았습니다. 1차 고역통과필터의 라플라스 표현은
입니다. 여기서 tau를 구하는 방법은
에서
를 이용하면 차단주파수를 결정하고 난 후 tau를 구할 수 있습니다.
만약 100Hz라고 하면 tau는 위와 같습니다.
그러면 위의 고역통과필터를 구할 수 있습니다. 이 필터의 Bode Plot을 그려보면....
입니다. 딱 저역통과필터와 좌우대칭이죠^^
f_cut = 100 w_cut = 2*np.pi*f_cut tau = 1/w_cut num = np.array([tau, 0]) den = np.array([tau, 1.]) w, h = sig.freqs(num, den, worN=np.logspace(0, 5, 1000)) plt.figure(figsize=(12,5)) plt.semilogx(toHz(w), 20 * np.log10(abs(h))) plt.axvline(f_cut, color='k', lw=1) plt.xlabel('Frequency (Hz)') plt.ylabel('Amplitude response [dB]') tmpTitle = 'High Pass Filter, cutoff freq. at ' + str(f_cut) + 'Hz in continuous' plt.title(tmpTitle) plt.xlim(1, Fs/2) plt.grid() plt.show()
이를 그린 Python 코드입니다. numpy는 np로 import했고, matplotlib.pyplot은 plt로 import 했습니다.
연속시간 영역에서의 1차 고역통과필터를 이산 시간 영역에서 구하기
위에서 구한 연속시간에서의 고역통과필터를 이산시간의 표현으로 바꾸고, 이를 z-domain에서 표현해 보도록 하죠^^
먼저 애초의 이 식을...
정리한 후~~
역변환하면 위와 같이 연속시간의 함수로 표현될 겁니다. 이를~~
차분방정식으로 표현하고~
정리한 다음~~~ z 변환해 주면 됩니다.^^
이런 공식으로 나타났네요^^
tau와 ts(ts=10000)를 대입하고서 보니 위와 같은 z-domain의 전달함수를 얻었습니다.
s-domain에서의 결과와 겹쳐 그려보니 비슷하네요~^^
num_z = np.array([tau/(tau+Ts), -tau/(tau+Ts)]) den_z = np.array([1., -tau/(tau+Ts)]) wz, hz = sig.freqz(num_z, den_z, worN=10000) plt.figure(figsize=(12,5)) plt.semilogx(toHz(wz*Fs), 20 * np.log10(abs(hz)), 'r', label='discrete time') plt.semilogx(toHz(w), 20 * np.log10(abs(h)), 'b--', label='continuous time') plt.axvline(f_cut, color='k', lw=1) plt.axvline(Fs/2, color='k', lw=1) plt.xlabel('Frequency (Hz)') plt.ylabel('Amplitude response [dB]') tmpTitle = 'High Pass Filter, cutoff freq. at ' + str(f_cut) + 'Hz in discrete' plt.title(tmpTitle) plt.xlim(1, Fs/2) plt.grid() plt.legend() plt.show()
디지털 필터 구현하기
이제 z-domain에서 구현된 함수까지 있으니.. 살짝 어떻게 코드로 구현할 것인지 보죠^^
먼저 Direct II Form입니다. 저기서 나오는 계수들을 구하면 되죠. 뭐 1차니까 a2와 b2는 영일겁니다.^^
위의 z domain에서의 식에서 계수를 바로 구할 수 있습니다. 위와 같이 말이죠^^ 혹은 차분 방정식으로 바로 구현할 수도 있습니다.
def direct2FormModel(data, a1, a2, b0, b1, b2): from numpy import zeros, arange result = zeros((len(data),)) timeZone = zeros((len(data),)) for n in arange(2, len(data)): sum0 = -a1*timeZone[n-1] - a2*timeZone[n-2] timeZone[n] = data[n] + sum0 result[n] = b0*timeZone[n] + b1*timeZone[n-1] + b2*timeZone[n-2] return result def differentialEqForm(data, a1, a2, b0, b1, b2): from numpy import zeros, arange result = zeros((len(data),)) for n in arange(2, len(data)): result[n] = b0*data[n] + b1*data[n-1] + b2*data[n-2] - a1*result[n-1] - a2*result[n-2] return result
위 함수는 저역통과필터 때도 보여드렸던 함수로 direct2ForModel은 위 그림의 Direct II Form을 구현한 것이고 혹은 그냥 차분방정식의 형태로도 구현된 것입니다.^^
시험 신호는 [바로가기]에서 구현한 것을 그대로 사용하도록 하죠^^
시험 신호를 FFT한 것입니다.
이제
num_z = np.array([tau/(tau+Ts), -tau/(tau+Ts)]) den_z = np.array([1., -tau/(tau+Ts)]) a1 = den_z[1] a2 = 0 b0 = num_z[0] b1 = num_z[1] b2 = 0. filteredSig = differentialEqForm(inputSig, a1, a2, b0, b1, b2) draw_FFT_Graph(filteredSig , Fs, title='direct2FormModel', xlim=(0, 500))
FFT를 적용해보면 간단하게 HPF가 제 동작을 한다는 것을 알 수 있습니다.
고주파수 대역만 남겨두고 저주파는 걸렀기 때문에 위 그림의 빨간색처럼 낮은 주파수 성분이 사라진 것을 알 수 있습니다.
# -*- coding: utf-8 -*- def toHz(value): from numpy import pi return value/2/pi def direct2FormModel(data, a1, a2, b0, b1, b2): from numpy import zeros, arange result = zeros((len(data),)) timeZone = zeros((len(data),)) for n in arange(2, len(data)): sum0 = -a1*timeZone[n-1] - a2*timeZone[n-2] timeZone[n] = data[n] + sum0 result[n] = b0*timeZone[n] + b1*timeZone[n-1] + b2*timeZone[n-2] return result def differentialEqForm(data, a1, a2, b0, b1, b2): from numpy import zeros, arange result = zeros((len(data),)) for n in arange(2, len(data)): result[n] = b0*data[n] + b1*data[n-1] + b2*data[n-2] - a1*result[n-1] - a2*result[n-2] return result def filterSimpleHPF(data, tau, Ts): from numpy import zeros, arange result = zeros((len(data),)) for n in arange(1, len(data)): result[n] = (tau*result[n-1] + tau*(data[n]-data[n-1]))/(tau + Ts) return result def draw_FFT_Graph(data, fs, **kwargs): from numpy.fft import fft import matplotlib.pyplot as plt graphStyle = kwargs.get('style', 0) xlim = kwargs.get('xlim', 0) ylim = kwargs.get('ylim', 0) title = kwargs.get('title', 'FFT result') n = len(data) k = np.arange(n) T = n/fs freq = k/T freq = freq[range(int(n/2))] FFT_data = fft(data)/n FFT_data = FFT_data[range(int(n/2))] plt.figure(figsize=(12,5)) if graphStyle == 0: plt.plot(freq, abs(FFT_data), 'r', linestyle=' ', marker='^') else: plt.plot(freq,abs(FFT_data),'r') plt.xlabel('Freq (Hz)') plt.ylabel('|Y(freq)|') plt.vlines(freq, [0], abs(FFT_data)) plt.title(title) plt.grid(True) plt.xlim(xlim) plt.ylim(ylim) plt.show() import numpy as np import matplotlib.pyplot as plt import scipy.signal as sig # Create Test Signal Fs = 20*10**3 # 20kHz Ts = 1/Fs # sample Time endTime = 2 t = np.arange(0.0, endTime, Ts) inputSig = 3.*np.sin(2.*np.pi*t) sampleFreq = np.arange(10,500,50) for freq in sampleFreq: inputSig = inputSig + 2*np.sin(2*np.pi*freq*t) plt.figure(figsize=(12,5)) plt.plot(t, inputSig) plt.xlabel('Time(s)') plt.title('Test Signal in Continuous') plt.grid(True) plt.show() draw_FFT_Graph(inputSig, Fs, title='inputSig', xlim=(0, 500)) # Design 1st Order Low Pass Filter f_cut = 100 w_cut = 2*np.pi*f_cut tau = 1/w_cut num = np.array([tau, 0]) den = np.array([tau, 1.]) w, h = sig.freqs(num, den, worN=np.logspace(0, 5, 1000)) plt.figure(figsize=(12,5)) plt.semilogx(toHz(w), 20 * np.log10(abs(h))) plt.axvline(f_cut, color='k', lw=1) plt.xlabel('Frequency (Hz)') plt.ylabel('Amplitude response [dB]') tmpTitle = 'High Pass Filter, cutoff freq. at ' + str(f_cut) + 'Hz in continuous' plt.title(tmpTitle) plt.xlim(1, Fs/2) plt.grid() plt.show() # Design 1st Order Low Pass Filter Z-Transform num_z = np.array([tau/(tau+Ts), -tau/(tau+Ts)]) den_z = np.array([1., -tau/(tau+Ts)]) wz, hz = sig.freqz(num_z, den_z, worN=10000) plt.figure(figsize=(12,5)) plt.semilogx(toHz(wz*Fs), 20 * np.log10(abs(hz)), 'r', label='discrete time') plt.semilogx(toHz(w), 20 * np.log10(abs(h)), 'b--', label='continuous time') plt.axvline(f_cut, color='k', lw=1) plt.axvline(Fs/2, color='k', lw=1) plt.xlabel('Frequency (Hz)') plt.ylabel('Amplitude response [dB]') tmpTitle = 'High Pass Filter, cutoff freq. at ' + str(f_cut) + 'Hz in discrete' plt.title(tmpTitle) plt.xlim(1, Fs/2) plt.grid() plt.legend() plt.show() # Implementation Signal a1 = den_z[1] a2 = 0 b0 = num_z[0] b1 = num_z[1] b2 = 0. filteredSig1 = filterSimpleHPF(inputSig, tau, Ts) filteredSig2 = differentialEqForm(inputSig, a1, a2, b0, b1, b2) filteredSig3 = direct2FormModel(inputSig, a1, a2, b0, b1, b2) draw_FFT_Graph(filteredSig1, Fs, title='filterSimpleHPF', xlim=(0, 500)) draw_FFT_Graph(filteredSig2, Fs, title='differentialEqForm', xlim=(0, 500)) draw_FFT_Graph(filteredSig3, Fs, title='direct2FormModel', xlim=(0, 500)) plt.figure(figsize=(12,5)) plt.plot(t, inputSig) #plt.plot(t, filteredSig1, 'k', label='SimpleHPF') #plt.plot(t, filteredSig2, 'c', label='DE') plt.plot(t, filteredSig3, 'r', label='D2F') plt.xlabel('Time(s)') plt.title('Filtered Signal in Discrete') plt.legend() plt.grid(True) plt.show()
오늘 사용한 Python 전체코드입니다.^^
'Software > Python' 카테고리의 다른 글
| matplotlib에서 한글 표현하기 (10) | 2016.11.12 |
|---|---|
| Python으로 구현해 보는 Band Stop Filter (6) | 2016.09.22 |
| Python으로 구현해보는 Band Pass Filter (18) | 2016.09.08 |
| Python으로 구현해 보는 디지털 저역통과필터 (1차 Low Pass Filter) (30) | 2016.08.26 |
| Python에서 보드 선도 Bode Plot 그려보고 그래프 있는 척 치장하기^^ (6) | 2016.08.24 |
| IPython Notebook에서 Markdown 사용하기... (6) | 2016.08.19 |
| Anaconda를 이용한 Python 설치와 Spyder의 편리함 (12) | 2016.08.05 |